Sylow p-group (Sylow p群) – 解析タネル

今日は帰省の準備をしてました. あと年内に終わらせたい事務的なこととか, なにし天気が悪いのでインドアで詰め込み作業です.

今日考察していたことを記録していきたいのですが, 今回は範囲が広範でp-Sylow群では収まりません. 忘れていた線型代数の基本的な命題も同時に示しています. 手始めにp-Sylow群について見ていく前に有限Abel群の構造を検証していきましょう.

———————————————

有理数係数の(m,n)行列Aを, 有理整数環ZをQ加群とみなしたときの環準同型f:Z^n→Q^mの表現とする(基底(xi)∈Z^n,(yi)∈Z^mは標準とする).
このZには作用Q×Z→Z ((q,x)→qx)が定義されていて,

L_A={x∈Z^n|f(x)∈Z^m}

とおく. f(x)=f(x_1,…,x_n)=Σ[j=1,n]a_jy_j=yだから, 今jを一つ固定してyの要素をA=(a_1,…,a_n)の一次結合で表示すると,

a_jy_j=y_j(a_1j,a_2j,…,a_mj) (y_j∈Z, a_ij∈Q, 1≦i≦m, 1≦j≦n)

となる. そこでa_ijを改めて既約分数表示

a_ij=q_ij/p_ij (p_ij∈N＼{0}, q_ij∈Z)

で表し, LCM(p_1j,p_2j,…,p_mj)=μ_j とおけば, y_j∈Zμ_jはa_jy_j∈Z^mとなるための必要十分. 同様のことが全ての1≦j≦nにわたって成り立つから,

LCM(μ_1,μ_2,…,μ_n)=σ

とおけば

σf(x)=f(σx)∈Z^m

すなわち剰余加群Z^n/L_Aは有限加群で, Ann_Z(Z^n/L_A)=Zσ.

例えば
A=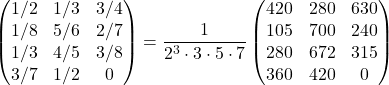 $\begin{pmatrix} 1/2 & 1/3 & 3/4 \\ 1/8 & 5/6 & 2/7 \\ 1/3 & 4/5 & 3/8 \\ 3/7 & 1/2 & 0 \end{pmatrix} = \displaystyle{\frac{1}{2^3\cdot 3\cdot 5\cdot 7}} \begin{pmatrix} 420 & 280 & 630 \\ 105 & 700 & 240 \\ 280 & 672 & 315 \\ 360 & 420 & 0 \end{pmatrix}$
$\simeq \displaystyle{\frac{1}{\sigma}} \begin{pmatrix} 1 & & {\bf 0} \\ & 5 & \\ & & 840 \\ {\bf 0} & & \end{pmatrix} (\sigma=2^3\cdot 3\cdot 5\cdot 7=840)$

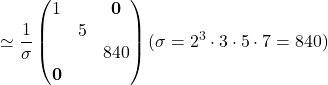
であるので, $L_A\simeq Z\oplus 168Z\oplus 840Z$ .

つまり剰余群Z^3/L_Aは

$Z^3/L_A\simeq Z/Z\oplus Z/168Z\oplus Z/840Z=Z/168Z\oplus Z/840Z$
と表され, (64,9,5,49)を一つの型として持つ. この型の表示では素因子型とSylow-p部分群G(p)(p=2,3,5,7)が容易に見れる(G(2)=Z/64Z, G(3)=Z/9Z, ..etc.). Z^3/L_AがAbel群であるからであるが.

このように, 有限のAbel群であればその明解な構造を位数から決定することができる. そこでAbel群の基本型(単因子型)の候補を位数から求めるために, 自然数nの分割が次のように与えられることを記しておきたい. 自然数nの分割P_nとは, 分割数をp(n)として

$\displaystyle{P_n=\Big\{(n_{i_1},n_{i_2},\ldots,n_{r_i}) |n=\sum_{j}^{r_i} n_{i_j}; 1\leq i\leq p(n) \Big\}}$

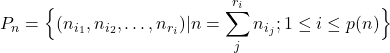
で表される集合のことをいい, P_1={(1)}, P_2={(1,1),(2)}, P_3={(1,1,1),(1,2),(3)}, P_4={(1,1,1,1),(1,1,2),(1,3),(2,2),(4)}, P_5={(1,1,1,1,1),(1,1,1,2),(1,1,3),(1,4),(1,2,2),(2,3),(5)}等となる. 分割数p(n)はその集合の濃度のこと.

位数2000のAbel群であれば, 2000=2^4*5^3だからその型の個数はp(4)p(3)=5*3=15個. すなわち位数nの型の個数が, nを素因数分解したときの各素数の冪数の分割数を乗じたものに等しくなる. 実際P_nから任意に分割を一つとってτ∈P_nとする. このときn(= $p_1^{i_1}p_2^{i_2}\cdots p_r^{i_r}$ )の素因数(p_1,p_2,…,p_r)に従って, $\tau=\displaystyle{ (\overbrace{p_1^{i_{1,1}},\ldots,p_1^{i_1}}^{p(i_1)\text{ patterns}},\overbrace{p_2^{i_{2,1}},\ldots,p_2^{i_2}}^{p(i_2)\text{ patterns}},\ldots,\overbrace{p_r^{i_{r,1}},\ldots,p_r^{i_r}}^{p(i_r)\text{ patterns}})}$
のようになり, 各素因数の積の表示パターンが分割数に等しいことが見れる.

———————————————

次に群準同型の列

$S:\begin{array}[c][/c]{ccccccccc} e & \stackrel{e_1}{\rightarrow} & G_1 & \stackrel{f}{\rightarrow} & G_2 & \stackrel{g}{\rightarrow} & G_3 & \stackrel{e_2}{\rightarrow} & e \end{array}$

を考える.

まずは「この列が完全であること」と「fが単準同型かつgが全準同型かつIm(f)=Ker(g)であること」が同値であることを見る.

列が完全であると仮定すると,

e_1:{e}→G_1はe→e’∈G_1

なる単準同型で(e→a≠e∈G_1だとすれば, (ee)=(e)→a^2が一般には成り立たない), Ker(f)=Im(e_1)={e’}からfは単準同型でないといけない.
またIm(g)=Ker(e_2)={x∈G_3|e_2(x)=e}=G_3からgは全射.

逆にfが単準同型ならKer(f)={e’}=Im(e_1)だし, gが全準同型ならIm(g)=G_3=Ker(e_2). 仮定からIm(f)=Ker(g)だからSは完全である.

※この最後の条件Im(f)=Ker(g)は重要で, これがないと逆が成り立ちません. 最初命題をこの条件なしで考えていて, 反例:

0→Z→Z→Z/2Z→0

(加法群の準同型列で, f:Z→Zを単準同型(恒等写像でいい), g:Z→Z/2Zを全準同型と仮定)

からIm(f)=Z≠2/Z=Ker(g))となるのに気づきました.

ところで群KからGへの単準同型 $\tau:K\hookrightarrow G$ の像がGの部分群になる. 実際Im(τ)∋y,zに対し, y=τ(a), z=τ(b)なるa, b∈Kがあって

yz^(-1)=τ(a)τ(b)^(-1)=τ(ab^(-1))∈τ(K)=Im(τ)⊂G

となることによる. このように群単準同型があるとき, Gの部分群をKと同一視できる.

群全準同型π:G→Kと単準同型τ:K→Gに対し,

πoτ=Id_K

を満たす単準同型τはπoτ(x)=x (∀x∈K)を満たすから, 明らかに左のような形になる.

この準備を以って次回群の半直積・正2面体群を考えていきます.

Merry Christmas★