他の解析的な問題に追われて後回しにしていました。ようやく時間が取れそうなので、ホモロジー群の考究をしていきます。
自分が辿った思考経路をそのまま残すことを優先させました。今回は基本的な事項について触れていきます。
間違いが結構あるかも知れません、勝手にそうだと解釈してる部分も多い気がします。
もし気づいたらご指摘いただけると幸いです。
—————————-
![]() を2次元複体とする.
を2次元複体とする.
境界準同型![]() に対し, 輪体群
に対し, 輪体群![]() , 境界輪体群
, 境界輪体群![]() である.
である.
実際![]() から2鎖
から2鎖![]() を取ると,
を取ると, 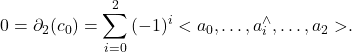 これが成り立つためには, 一時独立な向き付けられた単体
これが成り立つためには, 一時独立な向き付けられた単体![]() は全て0に等しくなければいけない.
は全て0に等しくなければいけない.
よって![]() また
また![]()
次に![]() から,
から, ![]()
その他ちょっとした検証から![]() であることが示されるが, 一応
であることが示されるが, 一応![]() のうち
のうち![]() となるものが存在することを確認しておく. それには
となるものが存在することを確認しておく. それには![]() とおいて
とおいて![]() なる2鎖
なる2鎖![]() の存在を示す.
の存在を示す.
そしてこれはやはり存在する. 境界準同型の性質から, ![]()
![]() である. 逆にこのような
である. 逆にこのような![]() が存在しないのは
が存在しないのは![]() のときで, このときまた
のときで, このときまた![]() である.
である.
ホモロジー群を構成しよう.
![]() をq次元ホモロジー群.
をq次元ホモロジー群.
全ての次元![]() に関するq次元ホモロジー群の直和を,
に関するq次元ホモロジー群の直和を,
![]() を複体Kのホモロジー群と呼ぶ. q次元ホモロジー群の元
を複体Kのホモロジー群と呼ぶ. q次元ホモロジー群の元![]() をq次元ホモロジー類と呼ぶ.
をq次元ホモロジー類と呼ぶ.
ここまでは定義どおり.
次を証明しよう.
![]()
なお, ![]() とはq次元複体からq単体を除いたものである. つまりこれはq-1次元複体である. またここで
とはq次元複体からq単体を除いたものである. つまりこれはq-1次元複体である. またここで![]() は整数環を表す(ここでは加群として考察するが).
は整数環を表す(ここでは加群として考察するが).
![]() であることに注意して,
であることに注意して, ![]() であるから, 0単体は無視すると,
であるから, 0単体は無視すると, ![]() が成り立つ.
が成り立つ.
結局左辺は,
![]() なるもの全体である. これが無限巡回自由加群となるから
なるもの全体である. これが無限巡回自由加群となるから![]() と同相なのは分かるが, それなら
と同相なのは分かるが, それなら![]() のいかなるq次ホモロジー群もそうではないの? と思ったら, どうもそのようである.
のいかなるq次ホモロジー群もそうではないの? と思ったら, どうもそのようである.
次に, m次元複体の2つのq輪体![]() がホモローグである場合の代数的表示がどうなるのか確認しておこう.
がホモローグである場合の代数的表示がどうなるのか確認しておこう.
このとき![]() である.
である. ![]() のときは明らかゆえ
のときは明らかゆえ![]() とすると,
とすると, ![]() から,
から, ![]()
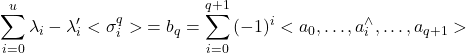 なる形に表せる
なる形に表せる![]() が存在する.
が存在する.
これでは今ひとつ見通しよく見ることができないが, 各単体は0ではないから基が同じなのは違いないようだ. 双方向きつき単体の同次一次形式で表されてる.
——————————-
次回位相不変量であるベッチ数の計算や部分複体の中で異なるベッチ数を持つものの関係などについて考察を加えたいと思います。