アフィン空間と図形 – 解析タネル

今日はアフィン空間について考えていきます。
ホモロジー群の続きをやろうと思うのですが、この辺の話を詰めながらの方が例にも取れるし順序的にはこちらの方がいいんでは？と思います。

間違い, 勘違い等がきっとあるでしょうから、もし気づいたらご指摘いただけると幸いです。

——————————————————-

アフィン空間はアフィン写像が定義できる空間で, 実際の世界でみれば3次元空間を2次元多様体と見做した(各点で2次元座標近傍が定義できるような)ものとされる. このように多様体と見做した定義では, 切り取った小さな部分の次元を言うので, 表現上の次元がひとつ下がる.

　
形式的に言えば, n次元実部分空間 $V$ で, 次のような座標対応 $\overrightarrow{*}$ と自己同型写像 $f$ が定義されるものを言う.
$Af=\{A,B,C,D\in V\subset R^n | \exists{f:V\mapsto V}; \vec{AB}=t\vec{CD} \Rightarrow f(\vec{B})-f(\vec{A})=tf(\vec{D})-tf(\vec{C}) (t\in R)\}$
　
実はこのような座標対応 $\overrightarrow{*}$ は, 数II・Bでベクトルを習っている人からすれば当然の結果だろう.
しかし $\overrightarrow{AB}=\vec{B}-\vec{A}$ と分解できることには, もちろんそのように定義された裏づけがある. 状況によっては $\overrightarrow{AB}=A\times B$ のようにベクトル積として変換を定義することもあるだろう (ただしこの場合アフィン空間とはならない. 実際このとき演算 $\vec{*}$ が重交代線形的であるから, $f(t\overrightarrow{AB})=t(A|B)\overrightarrow{ff}=0$ となっておかしい).

アフィン空間で問題とされるのは, 「方向」と「量」だ.
今その「量」にあたる体積が行列式 $\pm 1$ のアフィン変換(直交変換)によって変わらないことを見よう.

そのために, $a_1,\ldots,a_n \in R^n$ を辺とするn次元平行体 $P$ の体積 $V$ が, $a_1,\ldots,a_{n-1}$ を辺とする(n-1)次元平行体 $Q$ の(n-1)次元体積 $S$ と, $P$ の $Q$ に対する高さ $h$ の積になることを示す.

$P=\{\displaystyle{\sum^n_i{\lambda_i a_i}}|0\leq \lambda_i\leq 1\}\cdots (1)$ と表せることから, $v(P)$ は(n-1)次元閉区間 $I_{n-1}$ に基本変形
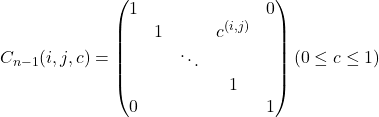$C_{n-1}(i,j,c)=\begin{pmatrix} 1 & & & & 0 \\ & 1 & & c^{(i,j)} & \\ & & \ddots & & \\ & & & 1 & \\ 0 & & & & 1 \end{pmatrix} (0\leq c \leq 1)$ を任意回適用させた集合の体積と等しい.
実際 $(1)$ で $n=2$ とすると, $I^2=(a,b)\times (c,d)$ に対し, $v(C_2(1,2,k)I^2)=\displaystyle{\int\int_{C_2(1,2,k)I^2}{dxdy}}=\displaystyle{\int^d_c\int^{b+ky}_{a+ky}{dxdy}}=v(I^2)$ であり, このときの $k$ がこの平行体における2辺の成す角の正接に等しい. このことが他の任意の2辺に対しても成りたつことは容易に確認できる.

まとめると, (n-1)次元閉区間 $I_{n-1}$ は体積を変えない基本変形の積として表される合同変換 $A_{n-1}$ に対し, 体積不変であり, (n-1)次元平行体 $Q$ とその体積を一致させることができる. 故に $V=Sh$ を得る.

さて, 次にこのようなアフィン空間にも群構造が定義されている例を見ていこう.
上記に示した $\vec{*}$ をはじめとした, 特定の演算を持つ集合の抽象化をすることで, 群ができた. 抽象代数的なアプローチが現実の幾何学(ユークリッド幾何)に還元するものは大きいが, 群を見ることでそれは一層はっきりする.

群の構造に関する定理のひとつである, 準同型定理は非常に興味深い性質を持ってる.

これはn次元ベクトル空間Vで定義される線形写像の階数に関する定理(次元定理):
　
$rankf=dimV-dim(Kerf\cap V)$
　
の一般化である.

まずその定理の内容から見てみよう.
　
$f:G\mapsto G'$ を準同型とすれば, 次が成り立つ: $G/Kerf \simeq Imf$
　
これだけとは実にシンプルだ.

一般的な証明は他所に譲って, まず準同型について考えてみよう. それは群 $G$ に関する2項演算 $\circ$ について, $G$ 上定義されている写像 $f$ の性質である. すなわち,
　
$(\forall a,b\in G)(f(a\circ b)=f(a)\circ f(b))\cdots (1)$
　
を満たすような $f$ のことである.

関数による演算を料理に例えるならば, 材料がパラメータ, 関数で像に値を写すことが調理にあたる. こういう言い方をすれば, 準同型とは材料を混ぜて調理しても, 材料を別々に調理しても, 最後に合わせればできるものは同じという性質だ.

なんともあたりまえのような気もするが, 調理の過程で失われるもの(水分等)やその量が, 調理の順序によって違いが生じることは想像に易い. ここでは $Kerf$ がその違いということになる.

準同型定理の興味深いところは, このような議論を群上の演算を $\circ$ と抽象化して表現できているところだ. つまり掛け算でも足し算でも, 群をなしうるのならば何らかの結合法則を勝手に決めてやってもいい. そうやって命題の表現を適宜制限してやればかなり具体的な問題に落とし込むことができるだろう.

例えば丸みを帯びた(桃のような)図形Pを, 内点を含む超平面 $\pi_a=\{x\in R^3 | (x|a)=c (a\in R^3, c\in R)\}$ で分割したとき, 分割した図形 $P_1 \cup P_2 = P$ のうち, どちらがくぼみ(溝の部分)を含むか, という問題を考えてみる. ただし $\pi_a$ によって分割される個数は2個であるとする.

この場合 i) $P_1,P_2$ ともに含む, ii) $P_1$ が含む, iii) $P_3$ が含む, の3つの場合が考えられる. 溝を表す曲線を $\phi :I\mapsto P (I=[0,1])$ とおけば, i)となる場合を $Im\phi$ 上の任意の一点 $\phi(t)(\forall t\in I)$ における接ベクトル空間が $\pi$ を含むこと, すなわち $TP_{\phi(t)}\supset \pi_a$ となることである. これは結局法線ベクトル $a$ が $(a|TP_{\phi(t)})=0$ を満たすことに等しい. ii), iii)の場合は, i)でない場合で $Im\phi$ に座標を入れたとき, その座標における向きを計算すればよい. 符号の違いがii)とiii)を分ける.

ここで実は, (i)を考察する際に準同型の概念が使える.
一つのパラメータを $\phi(t)$ における接ベクトルに固定させた内積 $(x|y)=g(x,y) (x\in P, y\in TP_{\phi(t)})$ を $g_t(x)=g(x,y)$ と同一視すると, 核 $Kerg_t$ を $TP_{\phi(t)}$ の法ベクトル空間 $TP_{\phi(t)}^{\perp}$ とみなすことができる. 念のため確認してみると, $g_t:P\mapsto R$ は加算について準同型である( $g_t(x+x')=g_t(x)+g_t(x')$ ). 従って $P/Kerg_t = P/TP_{\phi(t)}^{\perp} \simeq Img_t$ となる.

——————————————————-

次回にトポロジー的な内容で続きます。