多様体学習の応用を考える

未分類の高次元データから低次元表現を得る手法をDimensinal Reductionと言い、特に構造が複雑又は高次元のデータを、視覚的に ”意味の有る” データへ変換するアルゴリズムとして有力なものに NLDR (Nonlinear Dimensional Reduction) がある。

この記事では、Dimensional Reductionで視覚化可能なデータの構造について検証し、更なる応用について考える。

概要

未分類のデータのラベリングを考える際、特徴空間が低次元であったり対称性^[1]特徴の間の然るべき線形従属関係。を持てば、PCA (Principal Component Analysis) のような線形アルゴリズムによって特徴空間を少なくとも近似的に分割するアプローチがまずは有効と考えられる。

一方現実のデータには、特徴の種類が多すぎたり、特徴空間の構造 (i.e. 特徴同士の関係や各特徴が分類に与える影響等) が複雑である為に、効果的な “データ同士の近さ” を定義する事が難しい。

データの次元(intrinsic dimension)が大きくなる事で起こるこの現象は、しばしば “Curse of dimensionality” として知られ、適当な条件下でEuclid空間 (i.e. 線形空間) に顕著であることが分かっている¹。

非線形空間への埋め込みを経由して、データの特徴をできるだけ保ったまま次元の少ない空間に射影するアルゴリズムを多様体学習 = NLDR (Nonlinear Dimensionality Reduction) と言う。

この記事では、幾つかのNLDRアルゴリズムによるデータの視覚化を通じ、応用可能性の条件を模索する。

その為のデータとして基本的にはラベルあり (分類が予め分かっている) データを使用するが、ラベル (target) を与えなければラベル無し (各データの分類が未知である) データになるし、今回使用するアルゴリズムは本質的にラベルを必要としないので^[2]NLDRは教師無し学習アルゴリズムである。、実際の所区別する必要はない。

にも関わらず、現実のラベル有りデータには、与えられるラベルに間違いや曖昧さを含むケースが想定される。よって、多様体学習によってデータの特徴から導出した新しい分類と予め与えられた分類が、視覚的に一致している事を見るのは、少なくとも分析的なアプローチとしては有用だと考えられる。

またラベル無しデータについては、分類の候補を考えるのに役立つのではないかと思う。

NLDRの用途と制限

NLDRアルゴリズムにも様々なものがあり、特にその効果的な応用については良く知られていない事も多いようだ²。
しかしなぜNon-Linearなのか、なぜ教師無し学習アルゴリズムなのか、という点に着目すると、凡そ次のような事が言えるだろう:

次元 (intrinsic dimension) の高いデータの視覚化に効果的である。^[3]t-SNEアルゴリズムで視覚化可能なデータ構造について十分条件を与える結果がある (Theorem 4.1³)
導出されるデータ間の距離は相対的なもので、「何が」距離に寄与しているかの分析は一般に困難である。
他の手法 (Dimensional Reduction) に比べて計算コストが高く、機械学習パイプライン (i.e. 機械学習アルゴリズム・チェーン) に組み込むには用途が限られる。
データの相性が良ければ、前処理等に組み込む事で学習コストを下げられる場合がある。
NLDRでConcentration⁴を回避できるケースがあるが、万能では無く、最適な距離は結局データの構造に依存している³.

準備

インストール

Python 3.10とpipが入っている環境で検証を行っているが、Scikit-Learnを始めとする一連の機械学習パッケージが動作する環境であれば問題は無いはずである。

pip install --upgrade pip
pip install numpy scipy matplotlib ipython scikit-learn pandas pillow

基本関数の読み込み

以降データごとの視覚化の議論に注力する為、データの基本的な前処理やアルゴリズムの選択、視覚化を行う関数群は予め読み込んでおく。

モジュールダウンロード先: Github Repository

from a_module import *

データの可視化手順

今回行う技術的な検証の手順は以下の通りで、この手順をパラメタを換えて実行すれば良い。

赤文字は定義済みの基本関数で、3種類ある。

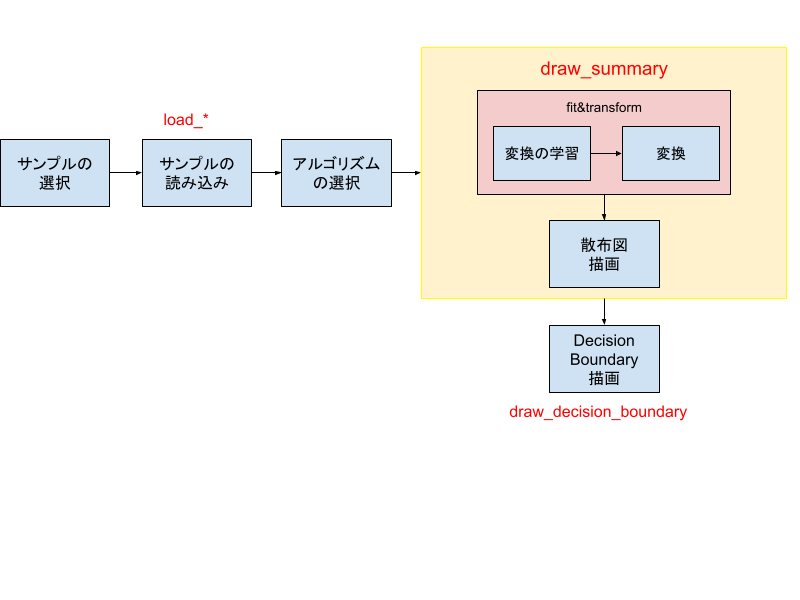
データセット

以下にデータセット (サンプル) を列挙する。

1~4はScikit-Learnが提供する公式のものである。

5はKaggleからdata setをダウンロードし使用する。
本記事ではモジュール (i.e. a_module.py ) の下に ./data/apple_quality.csv として保存している。

6は検証の目的で定義した3D Arrayを生成する関数である。

data set一覧

項番	名称	ID	データ種別	提供	基本関数名	ラベル
1	sklearn.datasets.load_digits	digits	画像	Scikit-Learn	load_digits	〇
2	sklearn.datasets.load_wine	wine	マトリクス	Scikit-Learn	load_wine	〇
3	sklearn.datasets.load_breast_cancer	bcancer	マトリクス	Scikit-Learn	load_breast_cancer	〇
4	sklearn.datasets.fetch_olivetti_faces	faces	画像	Scikit-Learn	load_faces	〇
5	Apple Quality	apple	マトリクス	Kaggle	load_apple_quality_csv	〇
6	Randomized 3D Coordinates	3ds	3D座標	custom	load_3ds	△ (ランダムに与える事は可能)

PCAによる可視化

まずは各データをPCA (Primary Component Analysis) アルゴリズムによって2次元に落とし、散布図と(ラベルがあれば)そのDecision Boundaryを見るのに次のコードを実行する^[4]Shellを使っている場合、描画の為に plt.show()というコードを付け加える必要がある。jupyter … Continue reading。

samples = load_xxx()

# scatter
_, reduced_samples = draw_summary(samples, decomposition.PCA)

# decision boundary
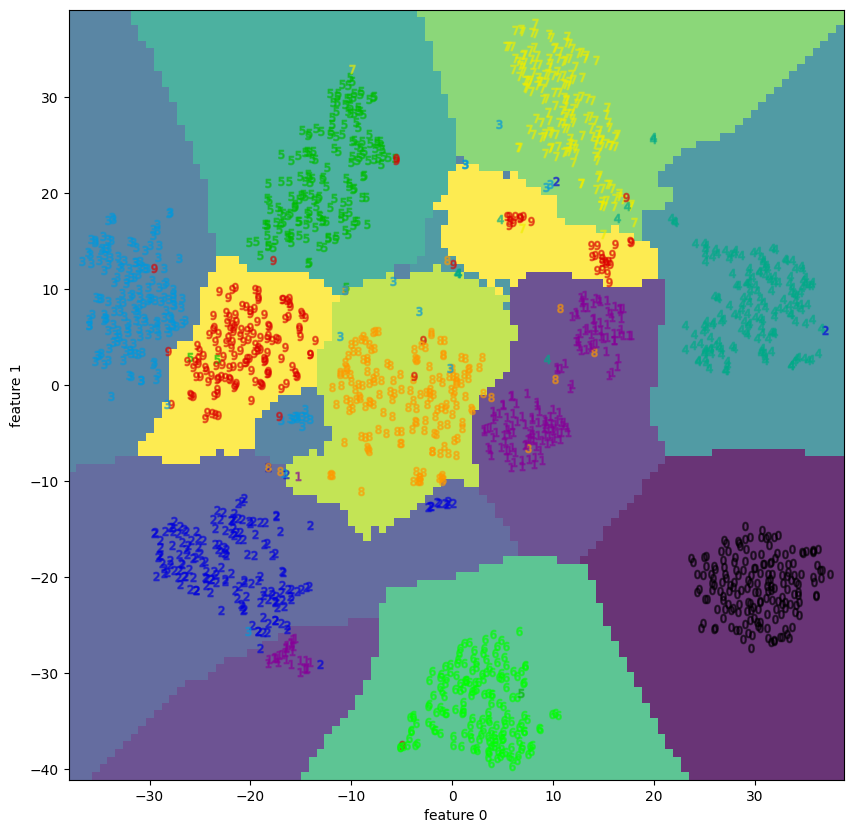
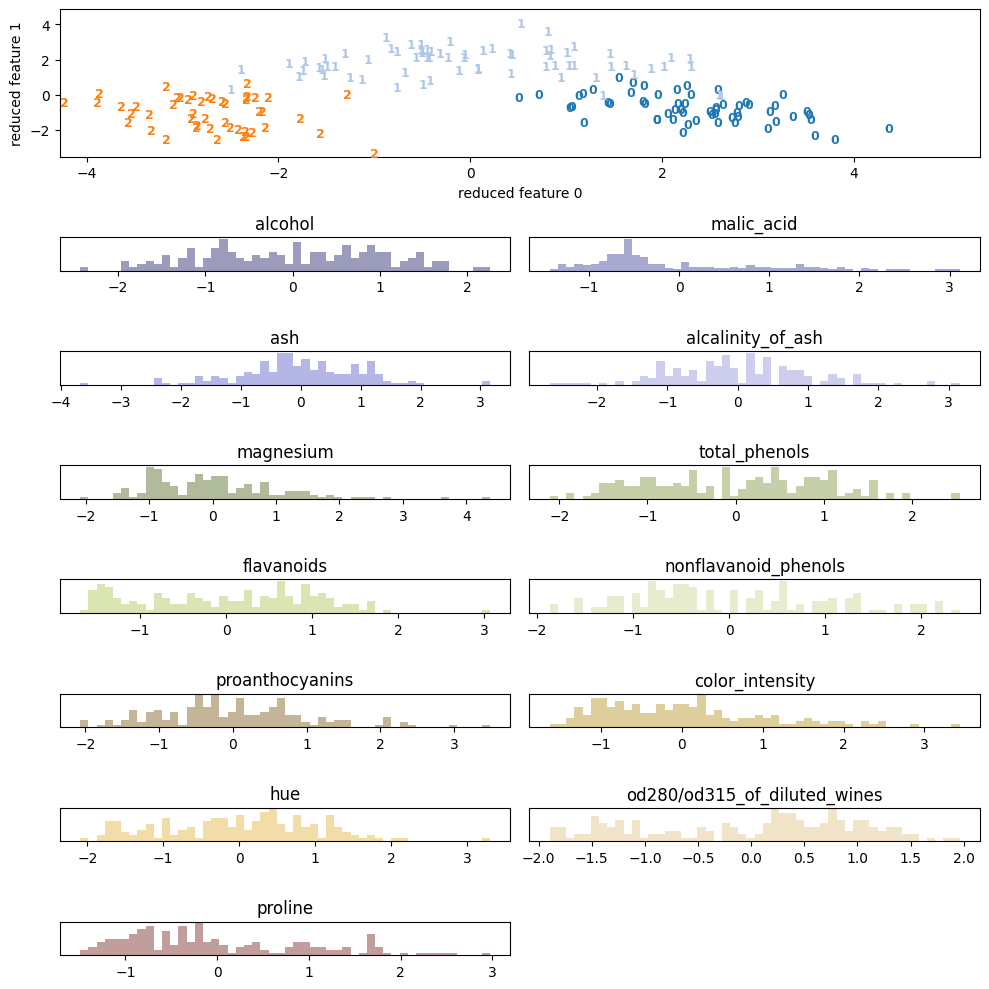
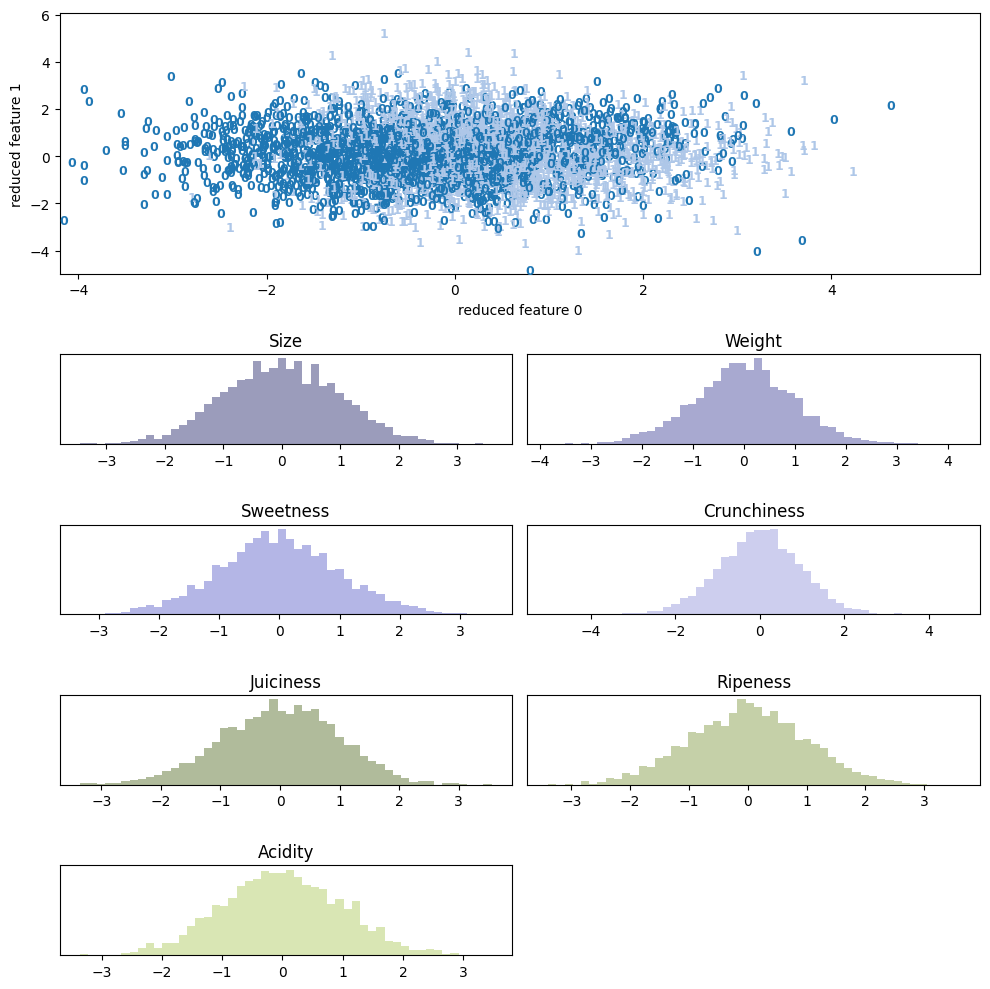
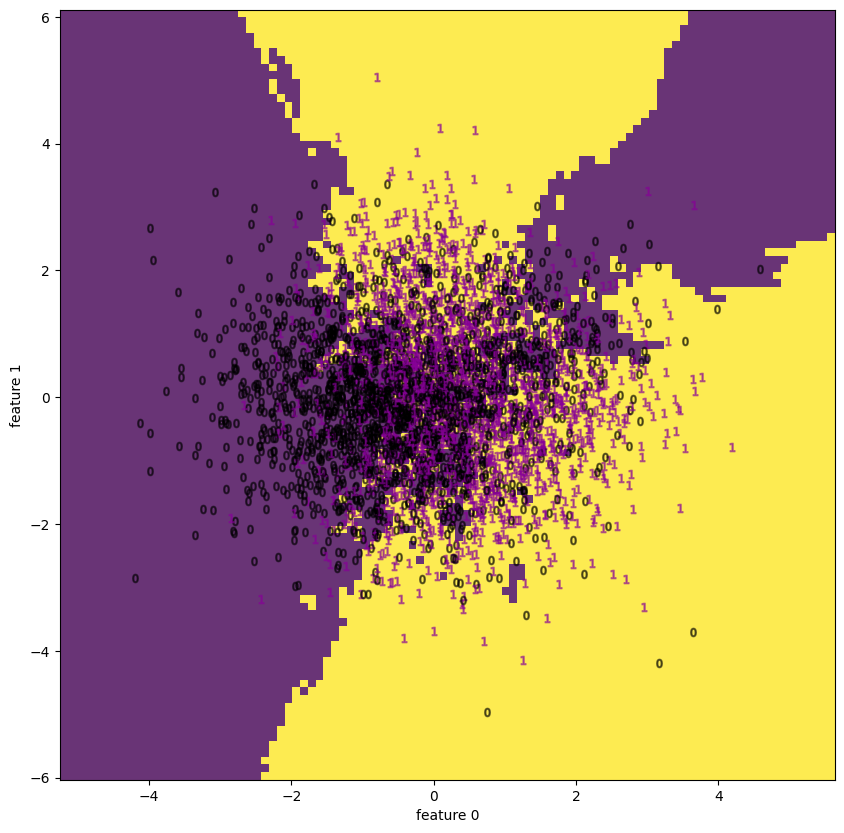
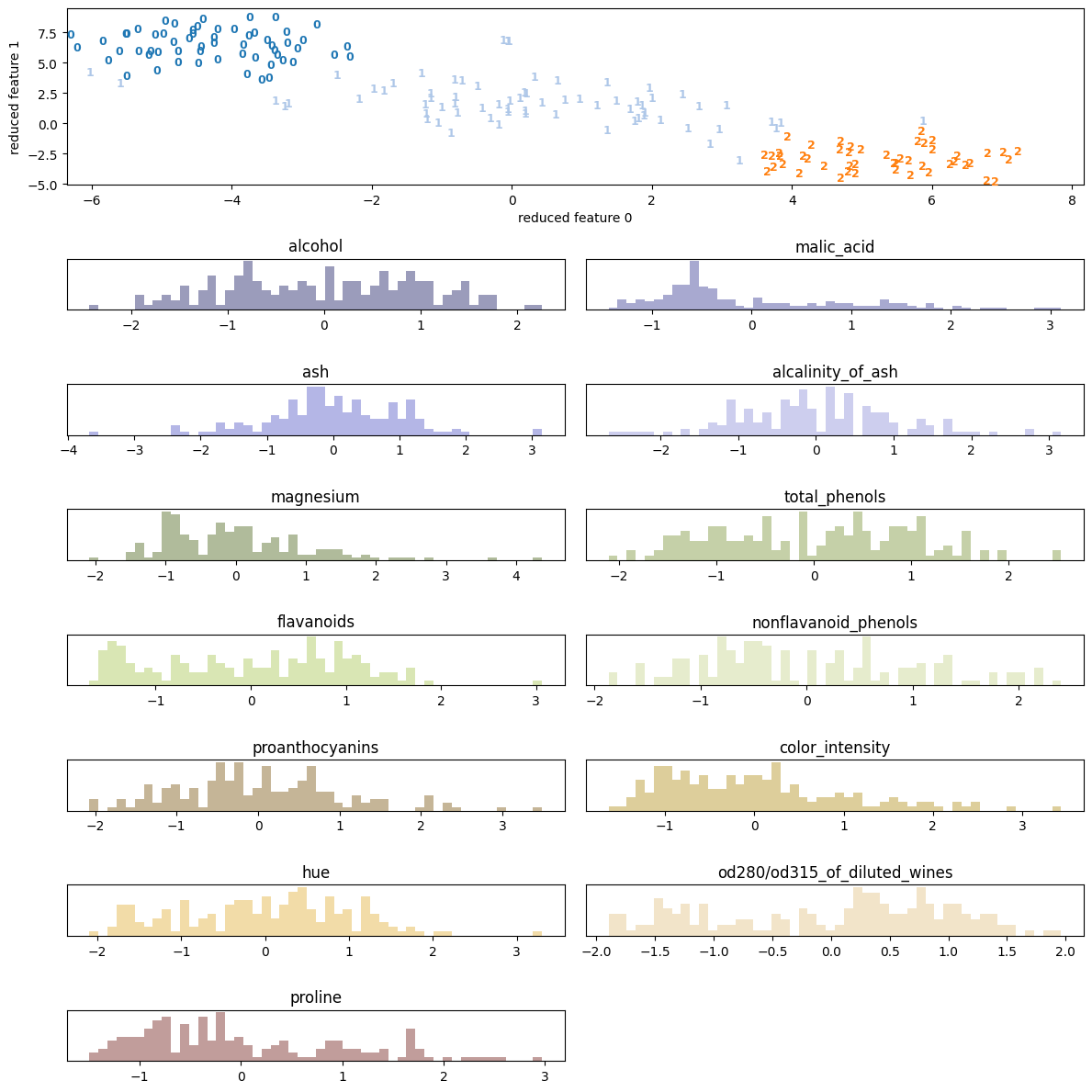
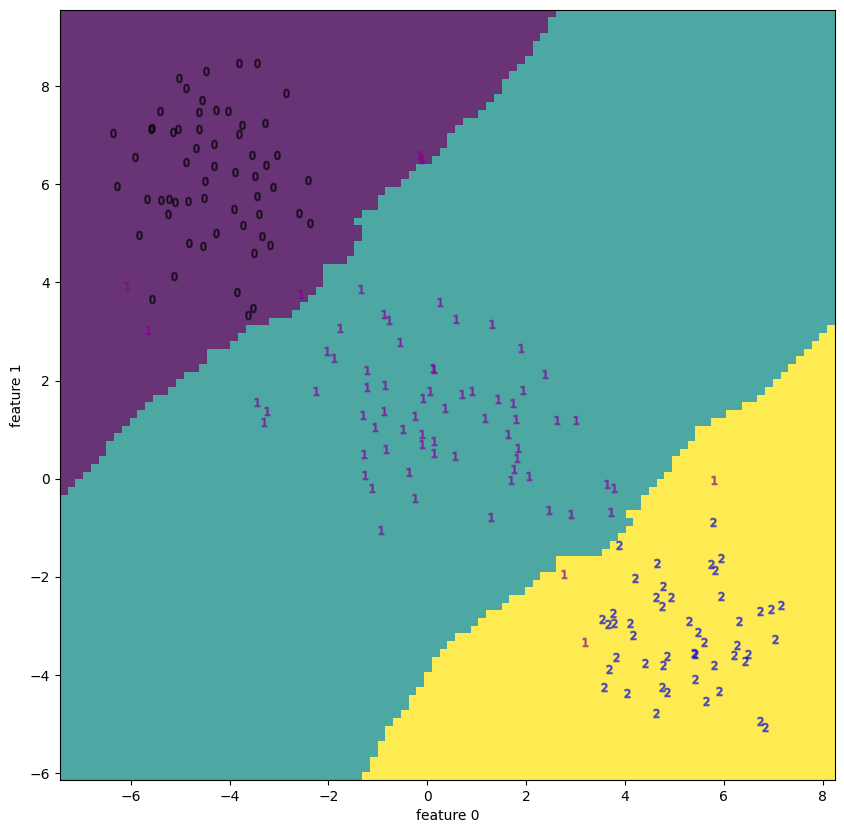
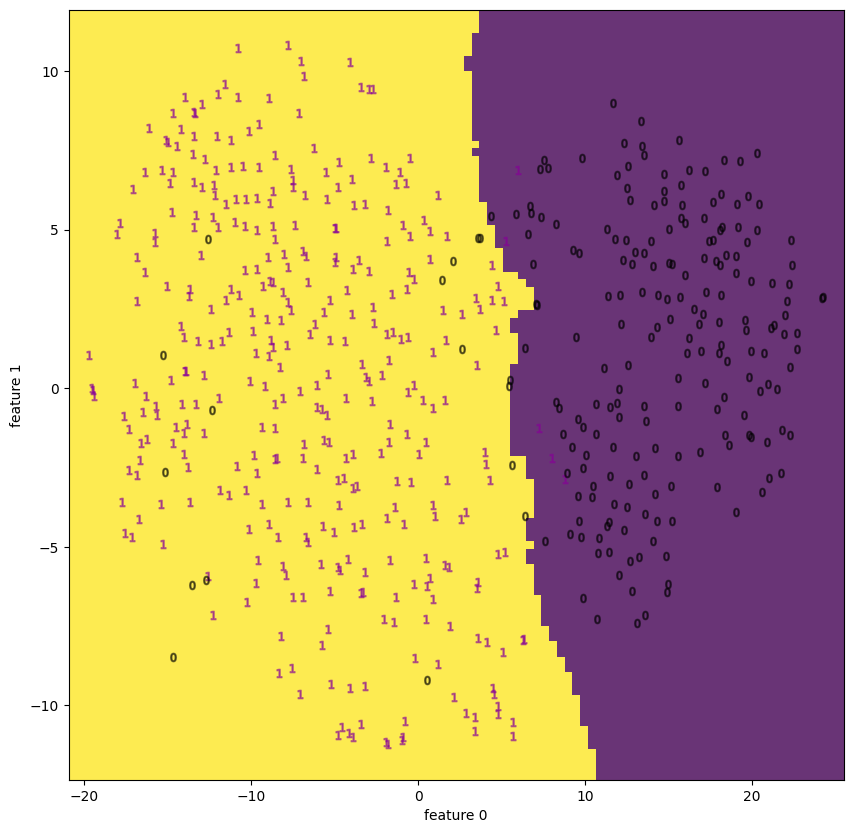
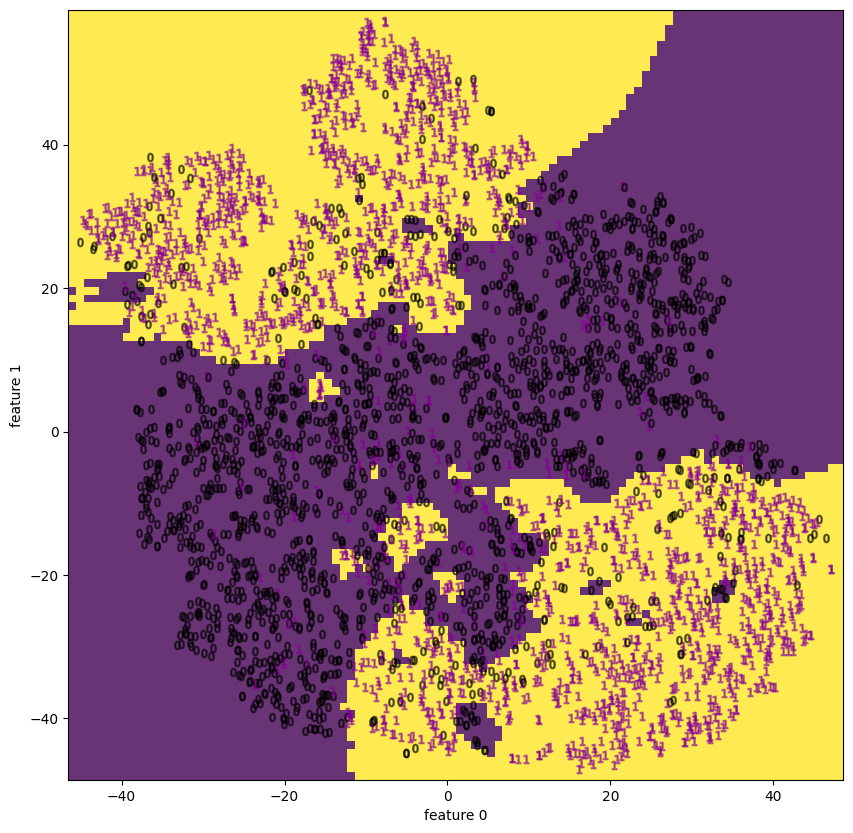
draw_decision_boundary(samples, reduced_samples)

load_xxxの部分を基本関数名で置き換えることで各サンプルの散布図を描画できる。結果は次のようである。

項番	ID	描画種別	パラメタ	画像
1.1	digits	scatter	None
1.2	digits	decision boundary	None
2.1	wine	scatter	None
2.2	wine	decision boundary	None
3.1	bcancer	scatter	None
3.2	bcancer	decision boundary	None
4.1	faces	scatter	None
4.2	faces	decision boundary	None
5.1	apple	scatter	None
5.2	apple	decision boundary	None
6.1	3ds	scatter	1000
6.2	3ds	decision boundary	N/A	N/A (適当なラベルが無い為)

考察

wineとbreast cancerについてはPCAで十分 (視覚的に) 分離できているが、それ以外はうまくいっていない。

特にdigitsは5, 8, 9等の数字がうまく分離できていない事が分かる。
関係を線形で記述できない変数 (特徴) が、原理的にPCAの結果にネガティブなインパクトを与える事を思えば、数字の周囲を囲む円の部分とその間の弧に相当する箇所のピクセルが影響しているように見える。

またwineでうまくいっていてappleでうまく行っていないのは、データの性質、特にラベルの性質も影響していそうだ。実際wineはワインの種類をラベル (target) にしているが(3種類)、appleではQuality (good / badの2種類) をラベルにしており、後者は恣意的な量である。

次に同じデータセットに対しNLDRによる可視化を行う。

この目的の一つは、PCAでうまく行かなかったケースについてNLDRの手法で視覚的に分離する事を見ることである。
しかしそれを見てもNLDRがPCAの代替になる事を示せるわけでは勿論無い。

むしろそれを踏まえて、NLDRの応用の可能性を探ることが主旨である。

NLDRによる可視化

NLDRと一括りに言っても知られているアルゴリズムだけでも幾つかあり、各々の背景理論等の詳細については私も殆ど良く知らない。

最近になって学習が可能になったとされるAutoencoderやLTSA¹ (Local tangent space alignment)は興味深いものの、分かりやすい結果を得るには技術的に解決しないといけない問題が幾つかある。

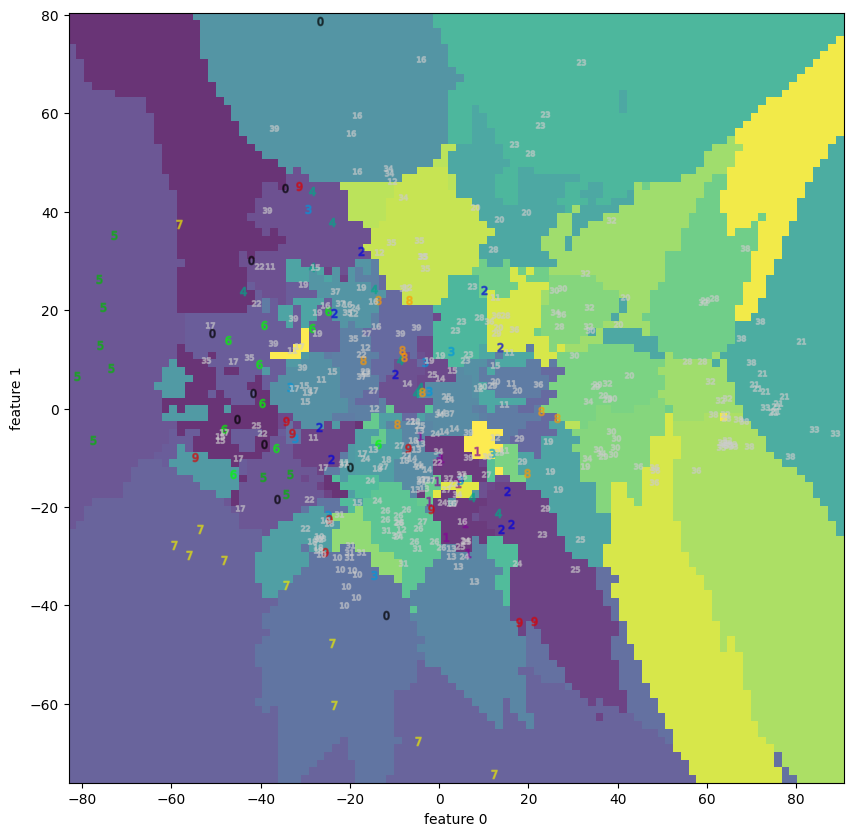
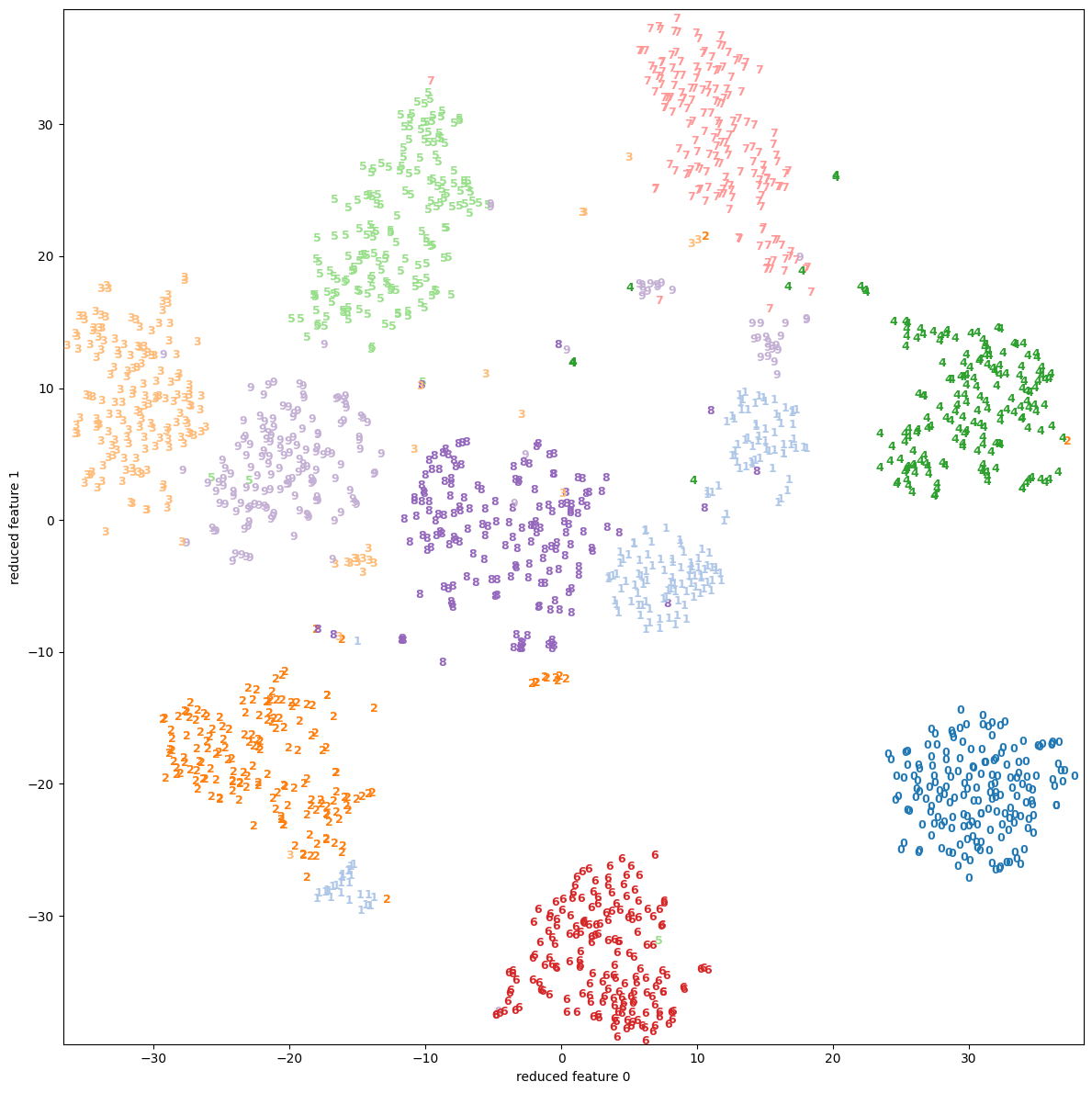
ここではNLDRによる視覚化の文脈で代表的に使われるt-SNEを使って検証を行う。

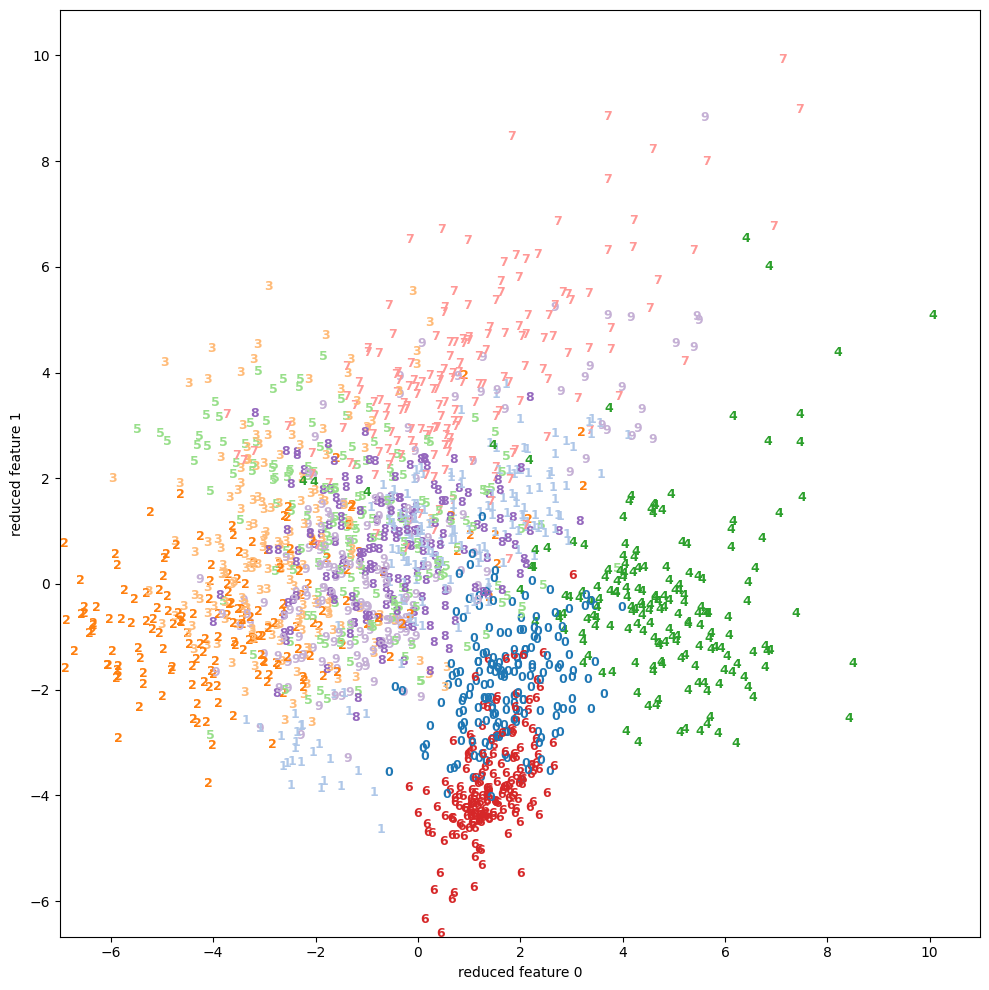
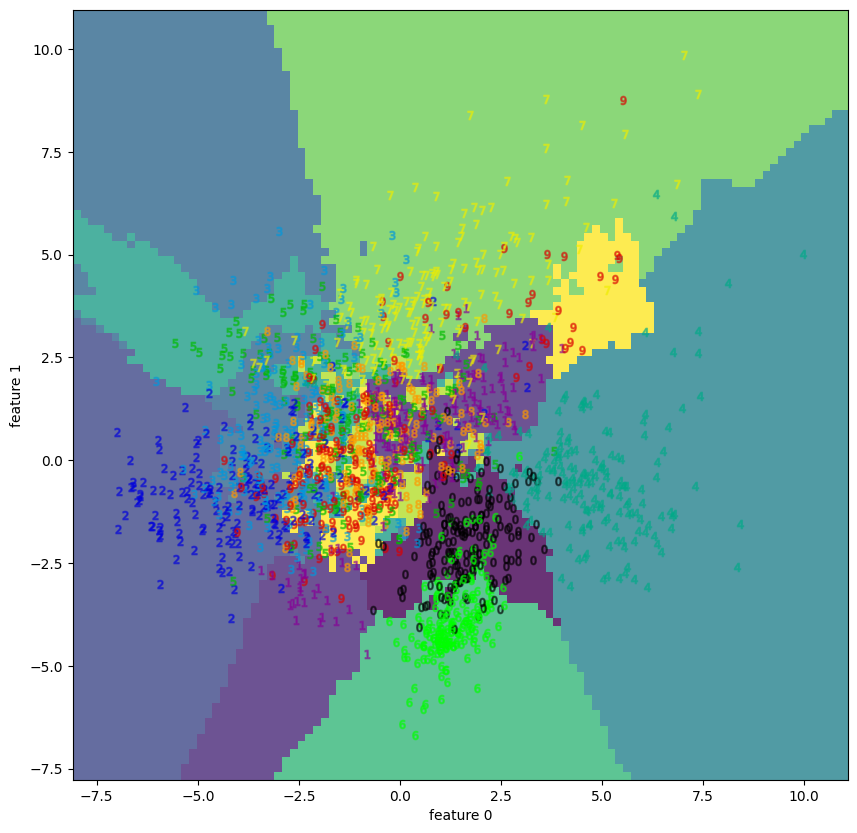
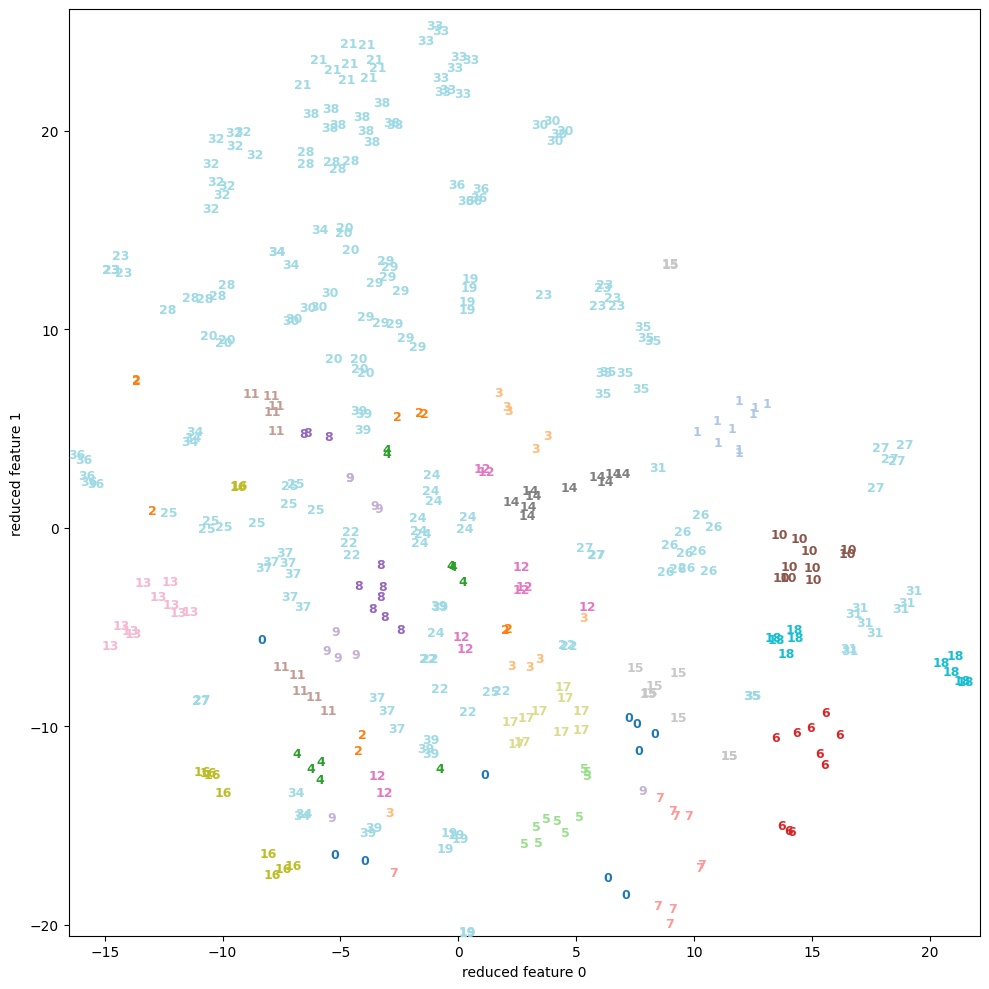
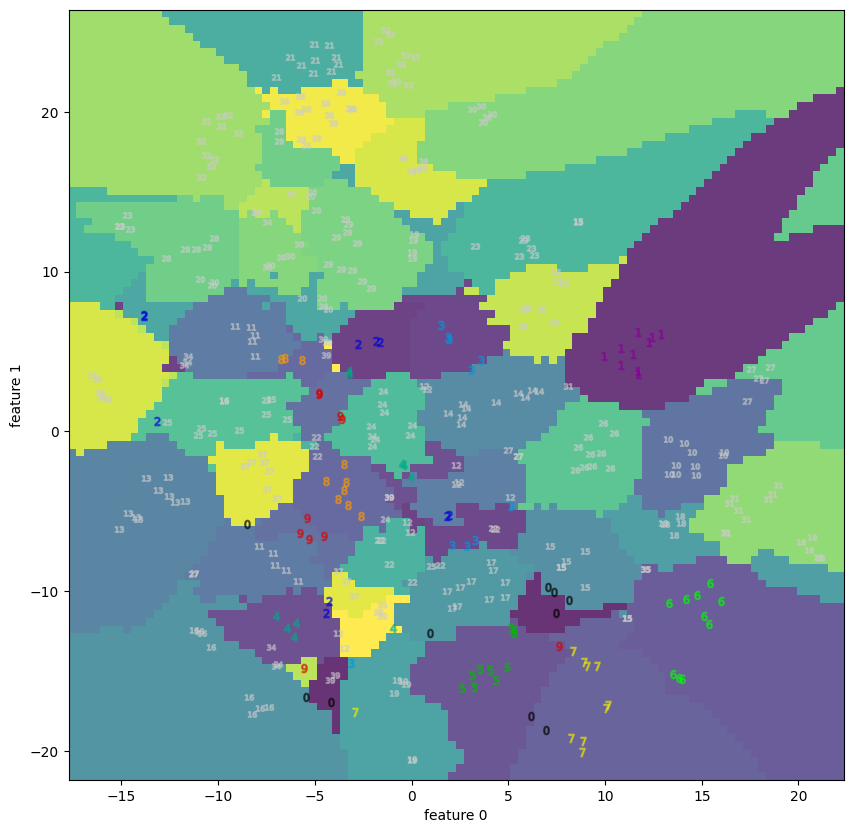
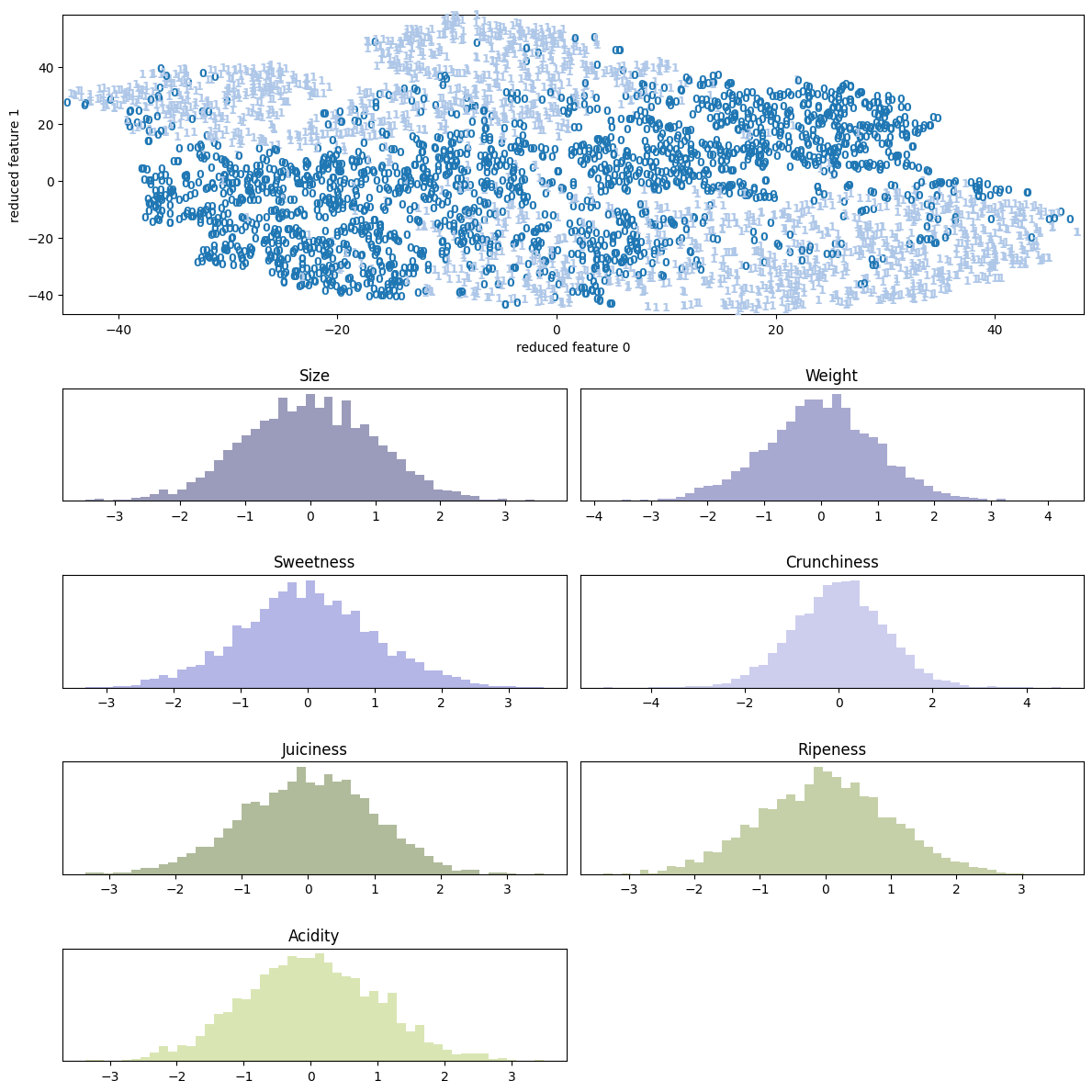
結果は次のようである。

項番	ID	描画種別	パラメタ	画像
1.1	digits	scatter	None
1.2	digits	decision boundary	None
2.1	wine	scatter	None
2.2	wine	decision boundary	None
3.1	bcancer	scatter	None
3.2	bcancer	decision boundary	None
4.1	faces	scatter	None
4.2	faces	decision boundary	None
5.1	apple	scatter	None
5.2	apple	decision boundary	None
6.1	3ds	scatter	1000
6.2	3ds	decision boundary	N/A	N/A (適当なラベルが無い為)

考察

PCAと比べると、多くのサンプルで(視覚的に)分離している様子を見ることができる。

特にdigitsやfacesには顕著で、appleも中央で1=”good”と 0=”bad”がごちゃ混ぜになっているようにも見えるが、Qualityの良いものは外側に広がっているので判別が付き易い。

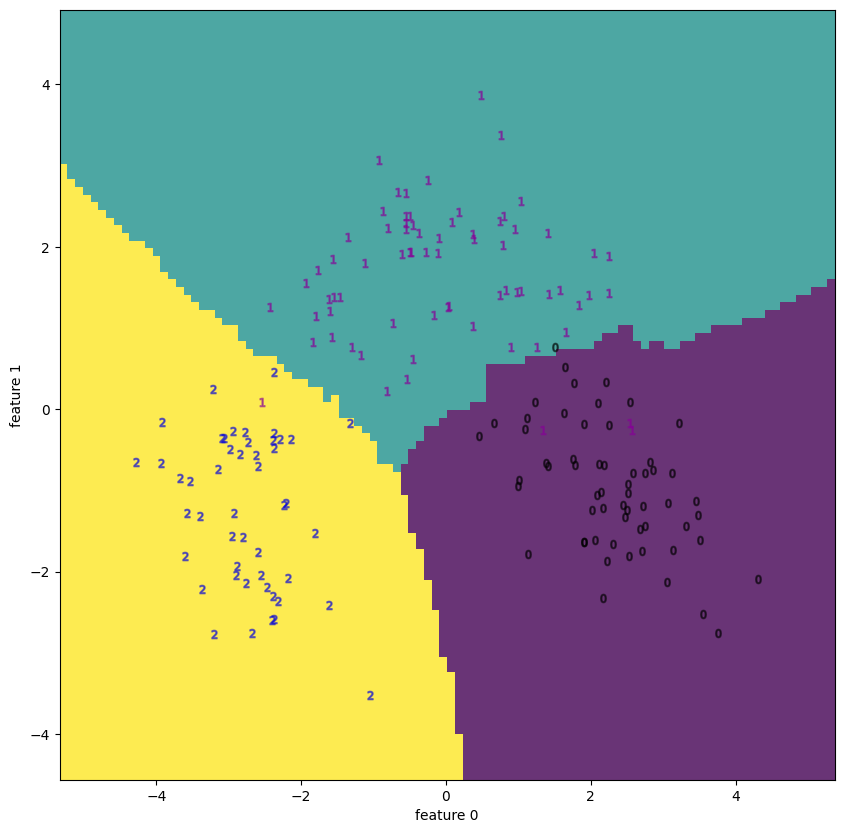
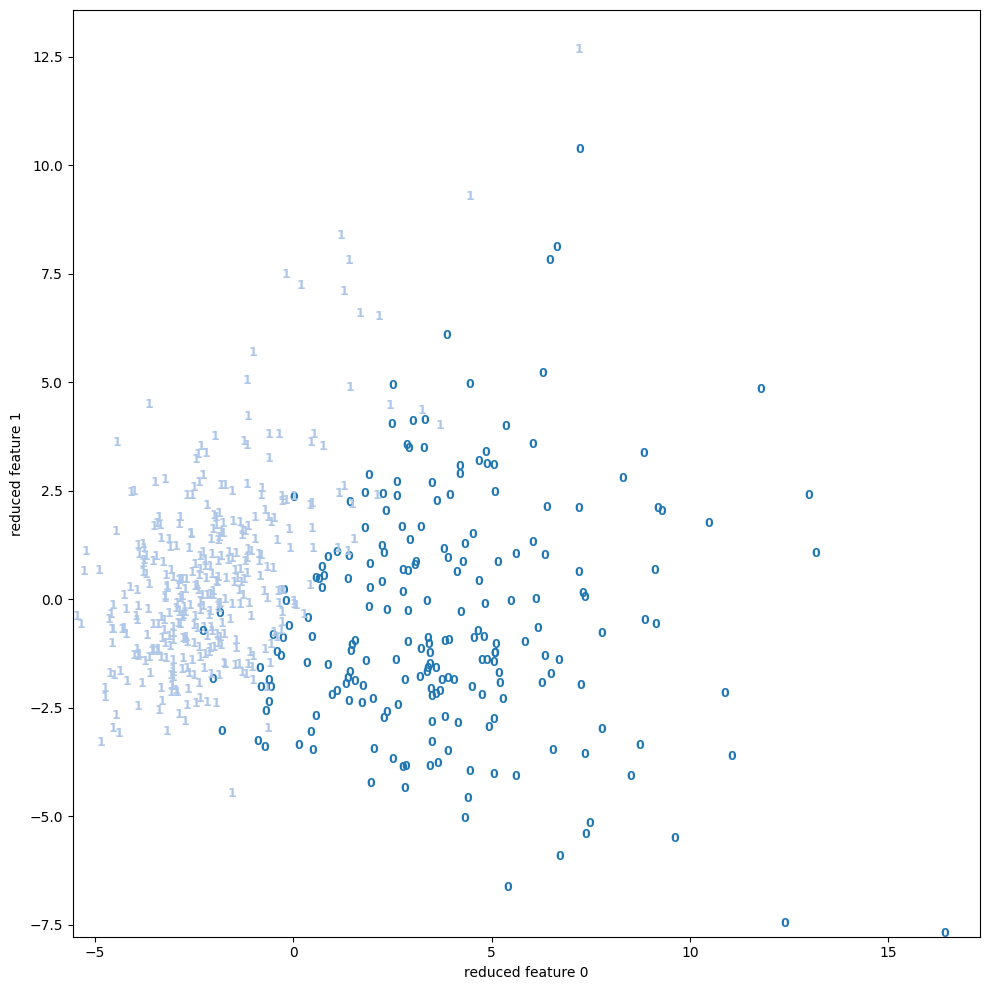
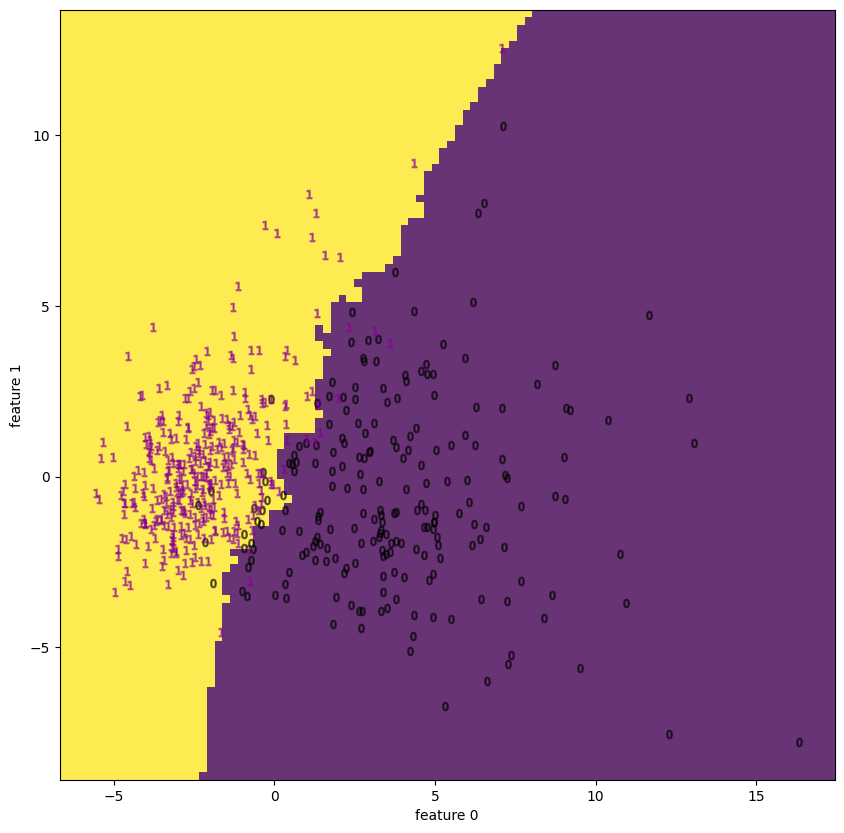
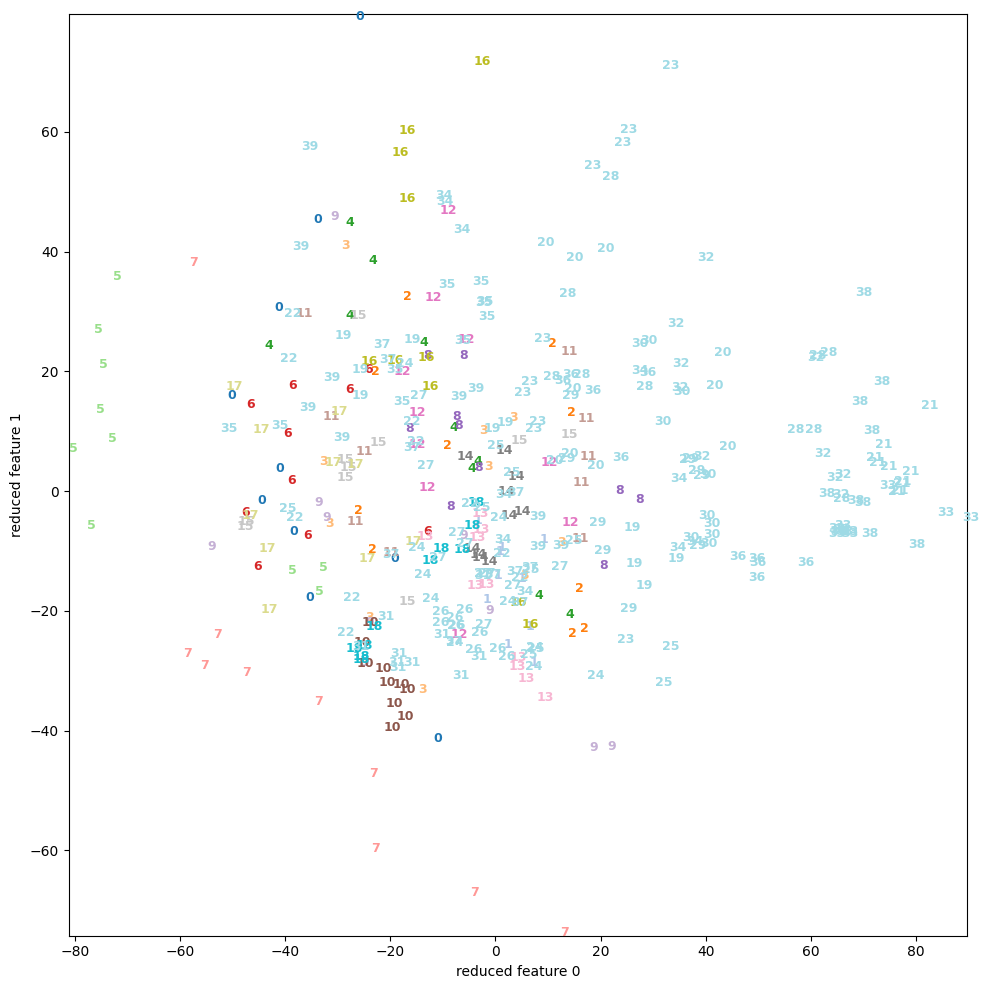
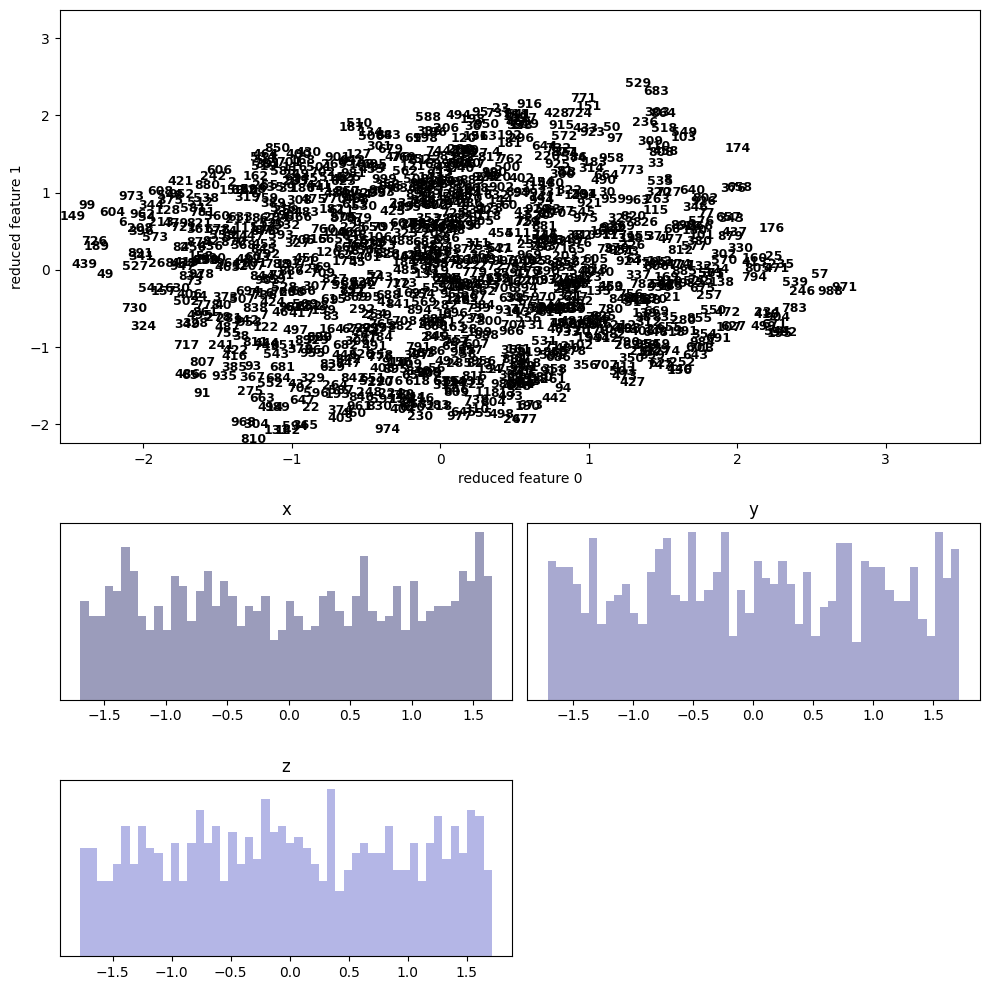
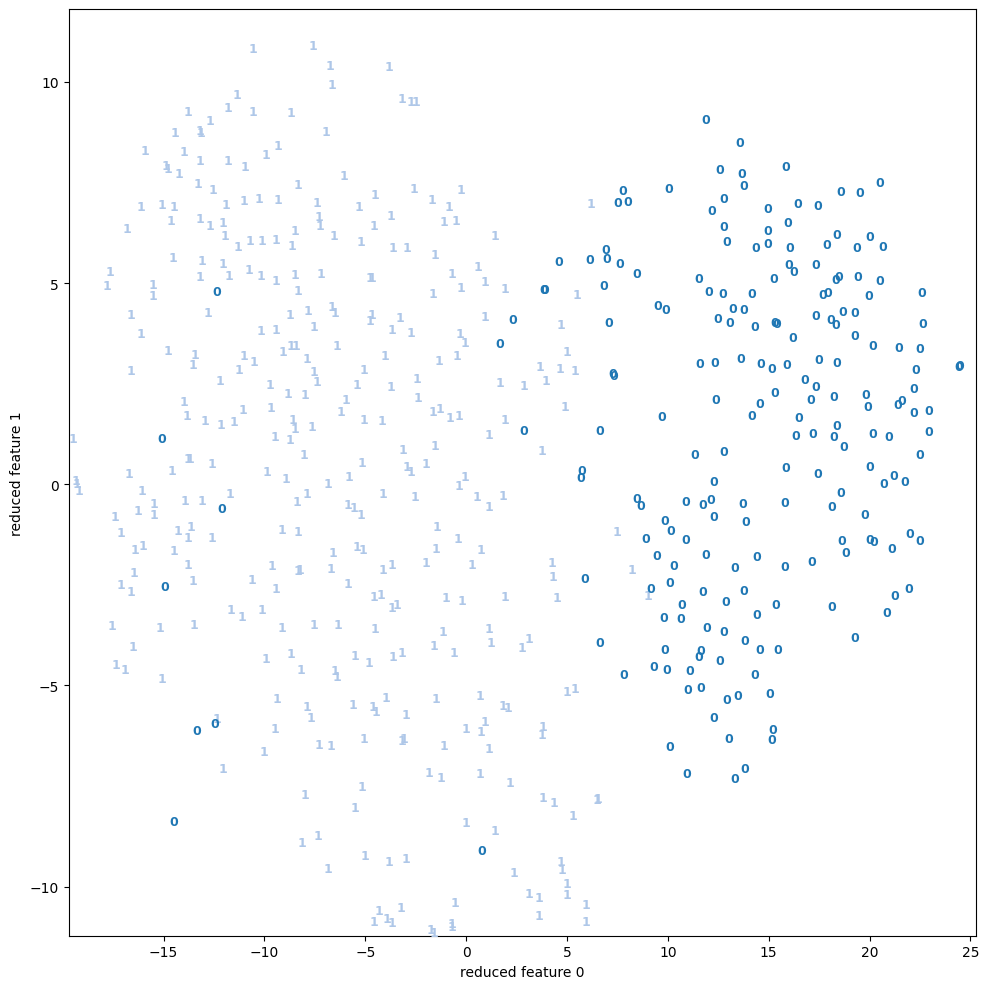
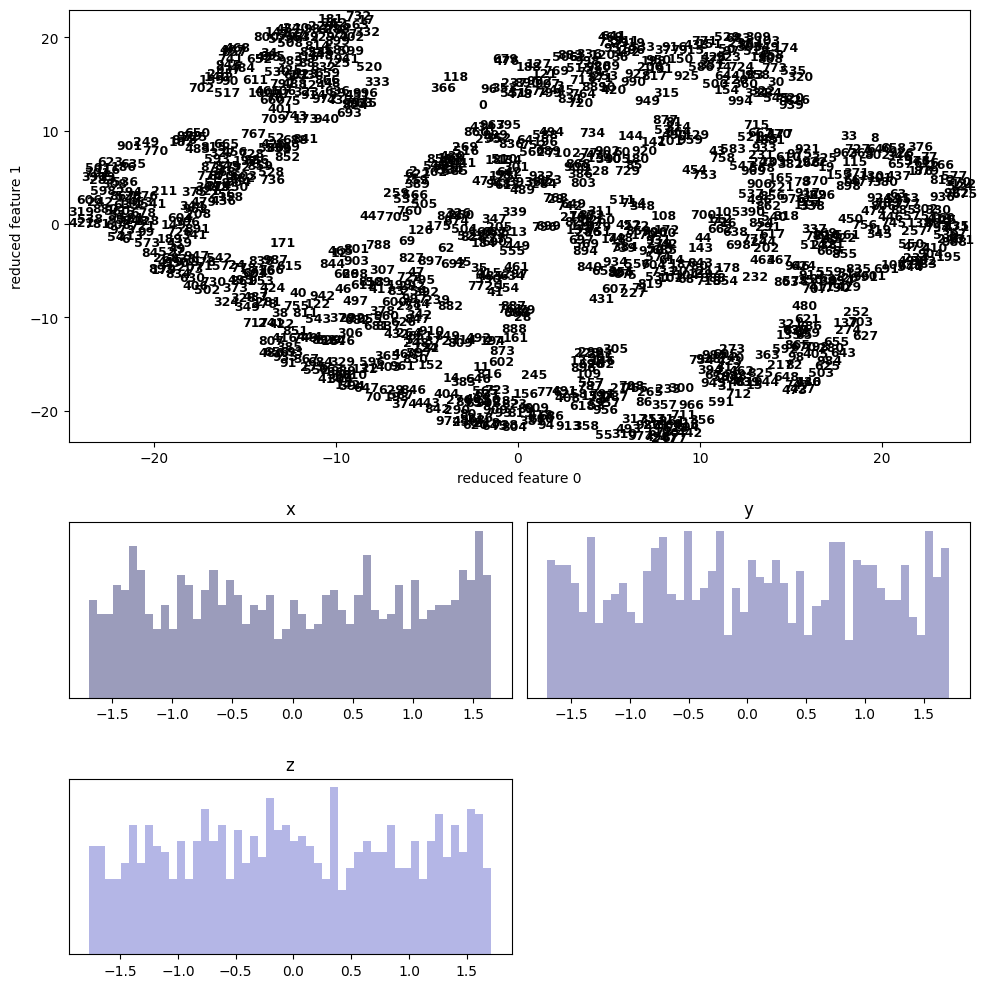
次の図は、6次元ベクトルデータ $v$ と線形変換 $T$ (6×6行列)を固定する時、第 $k$ 番目のデータを $T^{k-1}v$ で与えた100個のベクトルデータに対し、Dimensional Reductionを適用させた散布図である。

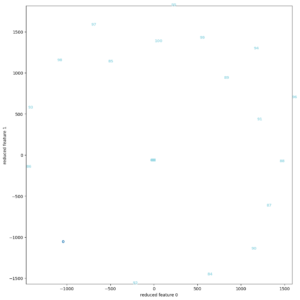
左図はPCA、右図はt-SNEである。
PCAによって算出された固有ベクトル (i.e. この場合x軸) 沿いにデータが集中している様子は、t-SNEが渦を巻く様に射影する結果と対照的で、その違いが顕著に表れている。

これらの例から、Dimensional Reductionの過程で非線形変換を経ることの優位性として、未分類データが、その特徴の相関に依存せず視覚的に分離され得る事を示唆する。

1.
Tenenbaum JB, de Silva V, Langford JC. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science. 2000;290:2319.
2.
Lee S, Laa U, Cook D. Casting multiple shadows: interactive data visualisation with tours and embeddings. Journal of Data Science, Statistics, and Visualisation. 2022;2. doi:10.52933/jdssv.v2i3.21
3.
Arora S, Hu W, K. Kothari P. An Analysis of the t-SNE Algorithm for Data Visualization. Published online 2018.
4.
Francois D, Wertz V, Verleysen M. The Concentration of Fractional Distances. IEEE Trans on Knowl and Data Eng. 2007;19:873–886. doi:10.1109/TKDE.2007.1037

Footnotes[+]

Footnotes
↑1	特徴の間の然るべき線形従属関係。
↑2	NLDRは教師無し学習アルゴリズムである。
↑3	t-SNEアルゴリズムで視覚化可能なデータ構造について十分条件を与える結果がある (Theorem 4.1³)
↑4	Shellを使っている場合、描画の為に `plt.show()`というコードを付け加える必要がある。jupyter notebookを使っている場合はそのままブラウザUI上に描画されるので便利である。