One found that there is the convention where ![]() denotes the upper-tail critical value such that
denotes the upper-tail critical value such that ![]() , as a standard notation in probability theory and, especially, in inferential statistics.
, as a standard notation in probability theory and, especially, in inferential statistics.
This value is often referred to as the upper ![]() -quantile or equivalently, the
-quantile or equivalently, the ![]() percentile.
percentile.
While the cumulative distribution function (CDF), ![]() , is fundamental in defining a probability distribution, the use of the right-tail probability for critical values has deep practical and historical roots in hypothesis testing.
, is fundamental in defining a probability distribution, the use of the right-tail probability for critical values has deep practical and historical roots in hypothesis testing.
Historical Background and Rationale
The primary driver behind this convention is its direct application in hypothesis testing, a framework largely developed by statisticians like Ronald A. Fisher, and Jerzy Neyman and Egon Pearson in the early 20th century. Here’s a breakdown.
Focus on “Significance”
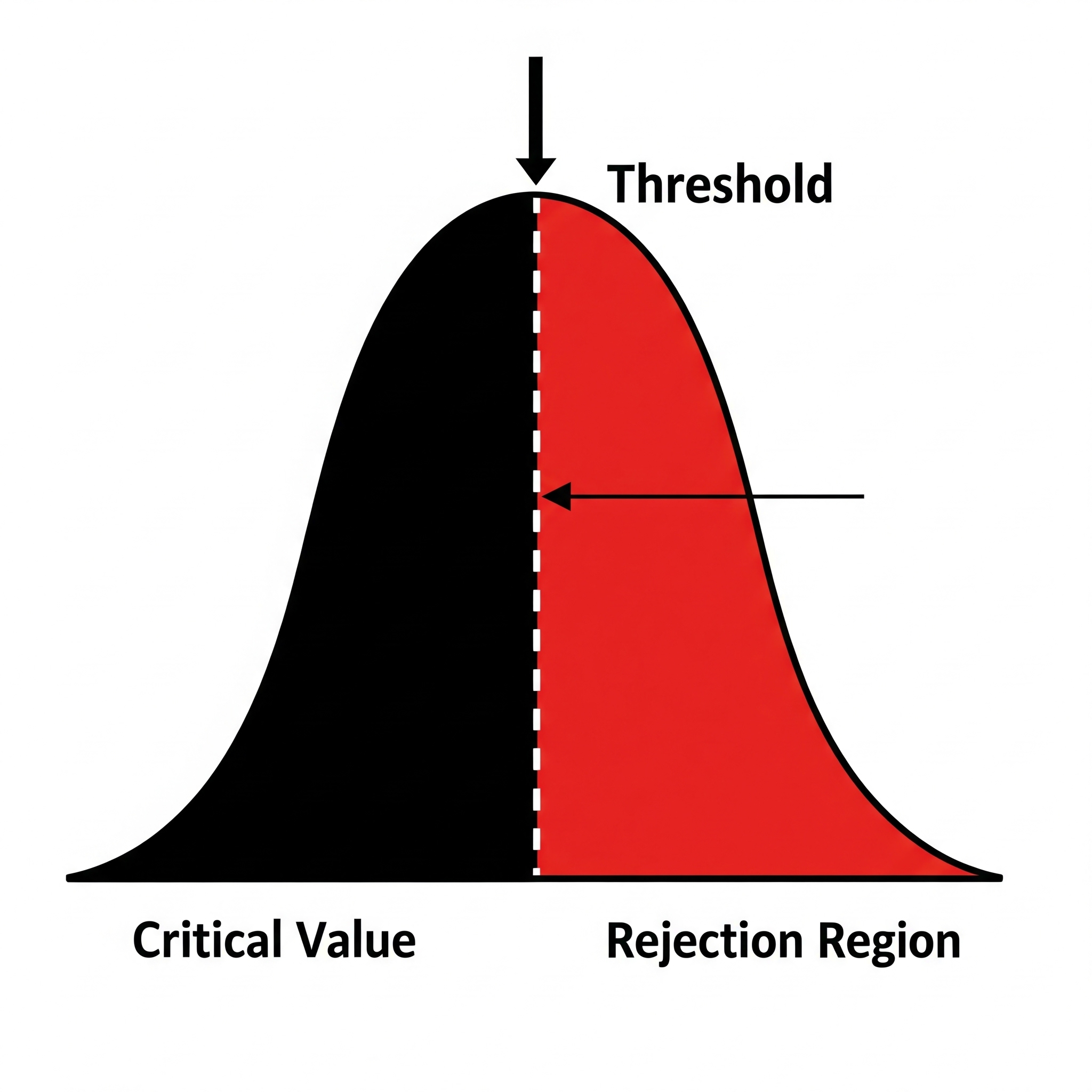
Hypothesis testing is centered around determining if an observed result is “statistically significant.” This often means checking if the result falls into a region of the probability distribution that is considered unlikely or extreme under the null hypothesis (![]() ). These extreme regions are typically in the “tails” of the distribution, while this does not directly explain why “the right-side” part.
). These extreme regions are typically in the “tails” of the distribution, while this does not directly explain why “the right-side” part.
Direct Comparison in Hypothesis Testing
When conducting a hypothesis test, you calculate a test statistic (e.g., a z-score). The decision rule is often to reject the null hypothesis if this statistic falls into the “critical region” or “rejection region.” This region is, in practice, often defined by the critical value ![]() . For an upper-tailed test, the rejection region is all values greater than
. For an upper-tailed test, the rejection region is all values greater than ![]() . Therefore, the notation
. Therefore, the notation ![]() provides a direct and intuitive link between the significance level (
provides a direct and intuitive link between the significance level (![]() ) and the critical value (
) and the critical value (![]() ) that defines the boundary of the rejection region, though this does not explain absolute necessity of “the right-sideness” in defining critical value.
) that defines the boundary of the rejection region, though this does not explain absolute necessity of “the right-sideness” in defining critical value.
The P-value Concept
The p-value can be interpreted as the probability of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is true. For a one-tailed test where large values of the test statistic provide evidence against ![]() , “at least as extreme” translates directly to
, “at least as extreme” translates directly to ![]() , where
, where ![]() is the observed statistic. The value
is the observed statistic. The value ![]() is the pre-specified significance level, which is the threshold for this probability.
is the pre-specified significance level, which is the threshold for this probability.
Deep in the p-value
Without limiting our scope to the one-tailed test, can we implicate highly plausible rationale of the right-sideness above the p-value concept?
Axiomatically, a p-value ![]() is a test statistic satisfying
is a test statistic satisfying ![]() for every sample point
for every sample point ![]() , by which the smaller values give evidence that
, by which the smaller values give evidence that ![]() is true, or equivalently, evidence of rejecting
is true, or equivalently, evidence of rejecting ![]() .
.
By restricting our target to the one that is called valid p-value, defined by a p-value that satisfies
![]()
we can explicitly construct the canonical p-value (i.e., “the most common way” of defining valid p-value) along with a given test statistic ![]() , where the large values of
, where the large values of ![]() give evidence that
give evidence that ![]() is true.
is true.
Theorem 8.3.27 (Casella, George, Statistical Inference 2nd edition).
For each sample point
, the function defined by
is a valid p-value.
In the above equation, by setting ![]() against each fixed sample point
against each fixed sample point ![]() and a given level
and a given level ![]() , it is reasonable to explain that the convention of using
, it is reasonable to explain that the convention of using ![]() for the right-tail probability became dominant in applied statistics because it aligns with the logic and application of hypothesis testing and defining critical regions of significance.
for the right-tail probability became dominant in applied statistics because it aligns with the logic and application of hypothesis testing and defining critical regions of significance.