Aboutを更新しました。
明確にテーマを限定して書いていこうという主旨です。
本記事の主題:
Fourier展開はLaurent展開の亜種(というかしょうなりいこーる)で、Fourier変換はその係数を求める操作です。周期関数はcosとsinで表示できるという触れ込みですが、範囲を狭めて局所的な表示だけを問題にするなら周期性は落とせます。構成的にはcosとsinでなくとも全平面で解析的な、あるいは問題としてる関数の定義されている集合で解析的な関数によって係数列を作れます(対数関数による巾級数など)。
———————————————–
■ フーリエ級数の存在
フーリエ級数論の主張は, ある領域で有理型(有限個の極を除いて解析的)関数がsinとcos, つまり波形の周期関数による級数表示が存在し, かつ一意的なことである.
通常周期関数の周期は最初に与えられているが, 任意の周期ωを持つ関数fが領域Ωで解析的であるという設定のもと, 複素フーリエ展開を考える.
領域Ωの任意点zに対しf(z+ω)=f(z)を満たすから, Ωをωの整数倍平行移動させた領域の上でも解析的で, 特に![]() .
.
故に代表の領域Ωとしては, まず原点を含む単連結領域を取っておけば良い(解析関数の局所写像性質より, 開領域を開領域に写す).
解析関数![]() によるΩの像は原点を含まない部分複素開領域Ω’であり, これをζ平面と呼ぶことにする.
によるΩの像は原点を含まない部分複素開領域Ω’であり, これをζ平面と呼ぶことにする.
ζは開円![]() と平行な帯
と平行な帯![]() をそれぞれ円環
をそれぞれ円環![]() と
と![]() に写し, 全平面を原点を除いた平面に写す. 従って原点を含む単連結領域をΩとして取る以上, ζ平面としては原点を含まない円環を考えれば良い.
に写し, 全平面を原点を除いた平面に写す. 従って原点を含む単連結領域をΩとして取る以上, ζ平面としては原点を含まない円環を考えれば良い.
この状況で領域Ωにおける解析(有理型)関数fに対応し, Ω’平面上の解析(有理型)関数Fが一意的に存在し,
![]()
を満たすというのである.
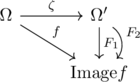
から見るように, 同様の性質を持つΩ’上の解析関数![]() が与えられ, これらが同じであるためには任意の
が与えられ, これらが同じであるためには任意の![]() に対し, 条件を満たすzが一意的に定まれば良い. これは
に対し, 条件を満たすzが一意的に定まれば良い. これは![]() をzについて解いて,
をzについて解いて, ![]() を得るので,
を得るので, ![]() が一価になるような枝を選んでやれば, ωの整数倍を除いて成立する. 実際任意にとったΩ’上の点ζを中心に, 半径
が一価になるような枝を選んでやれば, ωの整数倍を除いて成立する. 実際任意にとったΩ’上の点ζを中心に, 半径![]() の円の内部を
の円の内部を![]() と書けば,
と書けば, ![]() 上そのようにとれる. fの周期性からωの整数倍は消えるので,
上そのようにとれる. fの周期性からωの整数倍は消えるので, ![]() となる. ■ フーリエ展開の形 上記記号のもと, 必要なら原点を除いた円環Ω’の部分円環Η’とでも言うべきものをとり, この上でFは解析的とする. Cauchyの定理よりΗ’上Fはζの関数として原点を中心にLaurent展開できるから,
となる. ■ フーリエ展開の形 上記記号のもと, 必要なら原点を除いた円環Ω’の部分円環Η’とでも言うべきものをとり, この上でFは解析的とする. Cauchyの定理よりΗ’上Fはζの関数として原点を中心にLaurent展開できるから,
![]()
なる表示を得る(![]() はΗ’内の閉曲線).
はΗ’内の閉曲線). ![]() で変数変換して,
で変数変換して,
![]()
を得る.
ここでaはΩの任意点で, 道はΩ内でaからa+ωに至る任意の曲線で良い. よく知られるオイラーの公式により,
![Rendered by QuickLaTeX.com \[\begin{array}{lcl}c_n &=& \frac{1}{\omega} \int_a^{a+\omega} (\cos(2\pi nz/\omega)-i\sin(2\pi nz/\omega)) f(z) dz \\&=& \frac{1}{\omega} (-1)^n\int_{a-\omega/2}^{a+\omega/2} (\cos(2\pi nz/\omega)-i\sin(2\pi nz/\omega)) f(z) dz \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-1028c99823e0f1a22cb56ed1559e07e3_l3.png)
である. (複素)Fourier級数は,
![]()
nが負の項を整理して, ![]() なら
なら
![Rendered by QuickLaTeX.com \[\begin{array}{lcl}&& c_n \exp(i2\pi nz/\omega) + c_{-n} \exp(-i2\pi nz/\omega) \\ &=& (A-iB)(C+iS) + (A+iB)(C-iS) \\ &=& 2(AC+BC)\end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-9ee786c021f6a1dd3e52239a77512e9e_l3.png)
の形であるから, 正確には
![Rendered by QuickLaTeX.com \[\begin{array}{lcl}f(z) &=& \displaystyle{ c_0 + \sum_{n=1}^\infty \cos(2\pi nz/\omega)\cdot \frac{2}{\omega} \int_a^{a+\omega} \cos(2\pi nz/\omega) f(z) dz} \\ &+& \displaystyle{ \sin(2\pi nz/\omega)\cdot \frac{2}{\omega} \int_a^{a+\omega} \sin(2\pi nz/\omega) f(z) dz }\end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-79f661b954bb1bbbc49177ac6f52f327_l3.png)
という表現が得られる.