Note on extrema

by

For an optimization problem, we want to find an efficient way of calculating

  1. critical points (df)^{-1}(0);
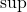  2. interior extremum \inf_{x\in(df)^{-1}(0)}f(x) (replace \inf with \sup, accordingly);
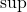  3. boundary extremum \inf_{x\in {\rm dom}(f)^{\bf b}}f(x) (replace \inf with \sup, accordingly).

For 1, the Newton’s method (and the variants) dominate in unconstrained case, while Sequential Quadratic Programming and Interior-Point methods are preferred in the constrained.

For 2, the Adaptive Trust-Region Methods remain most effective and widely used.

For 3, suggested SOTA approaches include augmented Lagrangian methods, where the trust-region framework is combined with a penalty term to enforce the boundary constraint, and Level Set methods (like stable homology).

In scenario 2, we are better to find the signature {\bf sgn}(d^2f)_a of quadratic form when

  • Adaptively control step sizes in optimization algorithms;
  • Gain a deeper understanding of the function’s curvature;
  • Improve the robustness and convergence of the concerned optimization process.

This can be seen in theory of local maxima and local minima, at the foundation.

note_on_extremaダウンロード