群論再考 – 解析タネル

Todd-Coxeterの方法というのがある. 与えられた有限群Gに対し自由群 $F_n$ からGへの全準同型を構成して構造と位数を決定する手法で, 最近これを使ってリー剰余群を調べているのだけど, 群の知識がぼやけていて少し復習がてらSylow-p群の項だけ構成的に書いてみることにする.

３年程前にSylow-p群について少し書いたことがあるが(Sylow-p群), 今見直してみると本質的なことがあんまり書かれていないので, 丁度いい機会になった.

◇可解群と冪零群の基本性質

Prop. 有限群G, $N\lhd G$ に対し, G/NとNが可解ならGも可解.
Pf. G/NのAbel正規列を $G/N=A_0/N\supset A_1/N \supset \cdots \supset A_m/N=N/N\cong 1$ とする.
Nを含むGの部分群とG/Nの部分群が一対一対応するから, $A_i$ とNが生成するGの部分群 $<a_i,n>=K_i$ と $A_i/N$ が対応する.
$K_0=G,\ K_m=N$ , $K_i/K_{i+1}\cong A_i/A_{i+1}$ はAbel群であるから, $G\supset \cdots \supset N$ までの正規列は $K_i$ で作れる. $N\supset \cdots \supset 1$ はNの可解性から作れる■</a_i,n>

Prop. Gが冪零群であることと, 中心化列で自明となるものがあることとは同値である.
Pf. まず $Z_0(G)=G,\ Z_{i+1}(G)=[G,Z_i(G)]$ とおいて, $Z_i(G)\lhd G$ を帰納法で示す. i=0なら $g[a,b]g^{-1}=[gag^{-1},gbg^{-1}]\in [G,G]$ で問題ない. k-1まで正しいとすると, $gxg^{-1}\in Z_{k-1}(G)\ (\forall g\in G, x\in Z_{k-1}(G))$ だから, 任意の $g,\ h\in G,\ x\in Z_{k-1}(G)$ に対し $g[h,x]g^{-1}\in [G,Z_{k-1}(G)]=Z_k(G)$ . よってkの時も示された.

中心化列で $G=Z_0(G)\supset \cdots \supset Z_n(G)=\{1\}$ となるものがあるとき, $Z_i(G)/Z_{i+1}(G)\subset Z(G/Z_{i+1}(G))\ (\forall i)$ を示せばこれは中心列であることが分かる.

自然な準同型を $\pi: G\rightarrow G/Z_{i+1}(G)$ とすると, $\forall g\in G,\ h\in Z_i(G)$ について,

$1_{G/Z_{i+1}} = \pi([g,h]) = \pi(g)\pi(h)\pi(g)^{-1}\pi(h)^{-1}$

∴ $\pi(g)\pi(h)=\pi(h)\pi(g)$ ■

逆にGが冪零群なら, 中心列 $G_0=G\supset G_1 \supset \cdots \supset G_n=\{1\}$ に対し, $Z_k(G)\subset G_k$ を示せば $Z_n(G)\subset G_n=\{1\}$ より中心化列を構成できたことになる. 帰納法を用いる.
まずk=0の時等号が成立する. k-1まで正しい, つまり $Z_{k-1}(G)\subset G_{k-1}$ とすると, $Z_k(G)=[G,Z_{k-1}(G)]\subset [G,G_{k-1}]$ である. $G_{k-1}/G_k\subset Z(G/G_k)$ だから, $gh=hg \mod G_k\ (\forall g\in G,\ h\in G_{k-1})$ である. これは $[G,G_{k-1}]=\{1\} \mod G_k$ を意味するので, $[G,G_{k-1}]\subset G_k$ である. よって示された■

◇Sylow-p群の基本性質

Gを有限群, $|G|=n=p^am,\ a>0,\ GCD(m,p)=1$ とする.

(i) Sylow-p群の存在

$p^a$ がnを割り切る最大のp冪であることを仮定してることに留意する. 元の数が $p^a$ であるようなGの部分集合全体をXとすると,
$G \curvearrowright X$ , つまりGがこの部分集合族Xに作用する. 実際 $g\in G, S=\{s_i\}_{1\leq i\leq p^a}\in X$ について,

$(g,S)\mapsto gS = \{gs_1,gs_2,\ldots, gs_{p^a}\}\in X$

はSを固定すれば準同型である. $p \nmid |X|$ が $p \nmid \binom{n}{p^a}$ より示せるので, これも前提とする.

Xを部分集合族XへのG作用で軌道分解すれば, $X=\bigsqcup_j GS_j$ (直和)となるので, $p \nmid |X|$ より $p \nmid |GS_k|$ となるkが取れる. $GS_k$ が上で説明した部分集合族Xへの作用に関する軌道であることを強調しておく. というのも, Gの自身への左作用によるGの部分集合Sの軌道は,

$GS=\{gs|g\in G,\ s\in S\}$

となり, 軌道の集合として元はGの元である. 一方部分集合族への作用によるG軌道は,

$GS=\{gS|g\in G\}=\{\{g_1s_1,g_1s_2,\ldots\},\{g_2s_1,g_2s_2,\ldots\},\ldots \}$

となるので, 軌道の集合として元がGの部分集合になる.

こうしてとった $GS_k$ に対し, ${\rm Stab}(S_k)=H$ とおくと, $|H|\mid |S_k|=p^a$ である( $S_k$ をHによって右分解し, $S_k=\bigsqcup_j Hs_{kj}$ と表せば分かる. $|Hs_{kj}|=|H|$ である). $p\nmid |GS_k|=|G/H|=|G|/|H|$ なので, |H|はnの最大p冪を因数として持たなくてはいけない. $|H|\mid p^a$ より $|H|=p^a$ である■

(ii) Sylow-p群は互いに共役/p群を含むSylow-p群が取れる

Sylow-p群Hを一つ固定し, 上で定義した元の数が $p^a=|H|$ であるGの部分集合族への作用として, 内部自己同型作用 $(g,S)\mapsto gSg^{-1}\in X$ を考える. この作用による $H\in X$ のG軌道を $O_G(H)$ とおくと, $O_G(H)$ はHと共役な部分群全体の集合に一致する. ${\rm Stab}(H)=N_G(H)\lhd G$ であるから, $G/N_G(H)\cong O_G(H)$ である(これは右辺が一般には群ではないので, 同型という意味ではなく, 同等という意味. また, Gがこの $O_G(G)$ にも部分集合として内部自己同型で推移的に作用することに留意する). $|N_G(H)| \mid |H|=p^a$ だが, 一般に $|H|\leq |N_G(H)|$ だから $|N_G(H)|=|H|=p^a$

∴ $p\nmid |O_G(H)|$ .

部分群 $K\subset G$ をp群とし, 先の内部自己同型による $O_G(H)$ をK空間と見做せる. $|K|=p^i$ なら, このK作用に関する軌道分解

$O_G(H) = \bigsqcup_j O_K(H_j)\ (H_j=g_jHg_j^{-1}\in O_G(H))$

を得るので, $p \nmid |O_K(H_t)|$ なるtを一つ取る( $p\nmid |O_G(H)|$ よりそのようなものは必ず取れる).
しかし, $|K|/|N_K(H_t)|=|O_K(H_t)|$ は, |K|がp冪位数であることにより, やはりp冪でないといけない. つまり
$|O_K(H_t)|=1$ を意味し, これは $kH_tk^{-1}=H_t\ (\forall k\in K)$ を意味する. すなわち $K\subset N_G(H_t)$

一般に $K, H\subset G$ が部分群で, $K\subset N_G(H)$ ならKHはGの部分群になる.
実際 $a_1,a_2\in K,\ h_1,h_2\in H$ なら, $a_i^{-1}=a_i^{-1}\cdot 1,h_i^{-1}=1\cdot h_i^{-1}\in KH$ .
そして $(a_1h_1)(a_2h_2)\in a_1a_2H$ だから演算が閉じている. また $kh\in KH$ に対し, $kh^{-1}k^{-1}\in H$ だから $(kh)^{-1}\in k^{-1}H$ である.

K, H共にHに内部同型で作用することから, $H_t\lhd KH_t$ を得る.

$|KH_t|$ はKの左作用による同等を考えると, $|KH_t|=|K|/|{\rm Stab}(H_t)|$ より|K|の約数, つまりp冪である.

同型定理より

$KH_t/H_t \cong K/K\cap H_t$

なので, $|KH_t|=|H_t|\cdot |K/K\cap H_t|$ . ここで $H_t\in O_G(H)$ はSylow-p群だから, $|KH_t|=|H_t|=p^a$ となる他ない.
このとき $|K/K\cap H_t|=1$ で, これは $K\subset H_t$ を意味する. よって任意のp群があるSylow-p群に含まれることが示された. 最初に $|K|=p^a$ ととっておけば, $K=H_t=g_tHg_t^{-1}$ だから, KとHは同じ共役類に属す■

(iii) Sylow-p群の個数は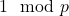 $1\mod p$

上でSylow-p群Hは固定したが, Sylow-p群全体の集合は先の命題により共役類に一致するためHに寄らない. 従って今後それを $\mathfrak{F}$ と書くことにすると, 示すべきことは共役作用による軌道の個数の等式 $|\mathfrak{F}|=|O_G(H)|=1\mod p$ である(Hは先ほど取った適当なSylow-p群). $\mathfrak{F}$ をH集合として軌道分解すると,

$|\mathfrak{F}| = \sum_j |O_H(H_j)| = \sum_j |H|/|N_H(H_j)| \ \cdots\ (*)$

が得られる. ここで $H=H_j\Rightarrow N_H(H_j)=H$ が分かるが, 実は逆も成り立つ. なぜなら $N_H(H_j)=H$ は $hH_jh^{-1}=H_j\ (\forall h\in H)$ と同値であり( $N_H(H_j)\subset H$ は定義から従うため), これは $H_j\lhd H$ と同値である. $|H_j|=|H|$ だから $H_j=H$ である.

以上から(*)の右辺において,

$|O_H(H_j)|=\begin{cases} 1 & (iff\ H=H_j) \\ p^r & (iff\ H\neq H_j,\ \exists r>0) \end{cases}$

が成り立つ. すなわち $|\mathfrak{F}|\equiv 1\mod p$ ■

———————————————————

prob. 位数30の群Gの同型類を決定せよ.
sol. この問題は一般にそれほど易しくない. 最も明らかな場合を示した後は, 方針等を記すに留める. $30=|G|=2\cdot 3\cdot 5$ だから, まず各素因数における適当なSylow-p群をD, E, Fとおいてそれぞれの個数d, e, fを決定する.
$D\cong Z/2Z,\ E\cong Z/3Z,\ F\cong Z/5Z$ で $d\equiv 1\mod 2,\ e\equiv 1\mod 3,\ f\equiv 1\mod 5$ が分かるが, d, e, fはD, E, Fの共役類の個数に他ならないので, $d=[G:N_G(D)]\mid [G:D]=15,\ e=[G:N_G(E)]\mid [G:E]=10,\ f=[G:N_G(F)]\mid [G:F]=6$ である. 先の条件と合わせて,

$\begin{array}{l} d\in \{1,3,5,15\} \\ e\in \{1,10\} \\ f\in \{1,6\} \end{array}$

最も簡単な状況として, $(d,e,f)=(1,1,1)$ がある. このとき $D,E,F\lhd G$ かつ各部分群の位数がどれも互いに素だから, GはSylow-p群の直積に分解する. つまり $G\cong Z/2Z\times Z/3Z\times Z/5Z \cong Z/30Z$ のときで, この時Gはアーベル群になる.

より明らかでない場合として, $(d,e,f)=(>1,1,1)$ を考察しよう. D, E, Fいずれも素数位数で巡回群だから, $D=<a>,E=<b>,F=$ と書くことにする. また, $E, F\lhd G$ で, DはGの正規部分群ではない. 位数とLagrangeの定理から, $G=DEF$ であることが分かる. $\xi:D\rightarrow {\rm Aut}E,\ \lambda:D\rightarrow {\rm Aut}F$ を内部自己同型で定めると, これらは同時には自明ではない. 実際両方同時に自明であるとき, DとE, DとFが可換となり, これはDが正規部分群でない仮定に反す. 今 $\xi,\ \lambda$ 両方共に自明でないと仮定する.
${\rm Aut}E=\{id_E,b\mapsto b^2\} \cong (Z_3)^\times$ , ${\rm Aut}F=\{id_F,c\mapsto c^2,c\mapsto c^3,c\mapsto c^4\} \cong (Z_5)^\times$ であるから, $aba^{-1}=b^2$ , $aca^{-1}\in \{c^2,c^3,c^4\}$ . $\lambda$ は単準同型で位数2の元aを位数が2の約数の元に写す. ${\rm Aut}F$ の置換表現は左からの合成を積とし, cの終域の次数を ${\rm Aut}F$ の元とみて( $c^i=i\ (i=1,\ldots,4)$ ), 同順で $<(1243)>=\{1,(1243),(1342),(14)(23)\}$ である. この巡回群の位数2の元は $(14)(23)$ のみで,

これは $c\mapsto c^4$ に対応する.

次に $\mu:E\rightarrow {\rm Aut}F$ を考えると, 同様の考察でこれは自明であるしかない. なぜならEの生成元bは位数3で, ${\rm Aut}F\cong <(1243)>$ に位数3の元は存在しないためである. 従ってEとFが可換であることが分かる.

以上から関係系

$G=<a,b,c|a^2=b^3=c^5=1,\ ab="b^2a,\" ac="c^4a,\" bc="cb">\ \cdots \ (*)$

</a,b,c|a^2=b^3=c^5=1,\>

を得る.

(*)から

$\begin{array}{lll} bab^{-1} =b^2a, & b^2ab^{-2}=ba, & \\ cac^{-1} =c^3a, & c^2ac^{-2}=ca, & \\ c^3ac^{-3} =c^4a, & c^4ac^{-4}=c^2a \end{array}$

を得る. このときSylow-2群の共役類に属す元の個数は

$O_G(</a><a>)=\Bigg\{ </a><a>, , <b^2a>, ,\ldots,<c^3a>, ,\ldots, <c^3b^2a> \Bigg\}$

</c^3b^2a></c^3a></b^2a>

の15個. Gの元は $c^ib^ja^k\ (i\in [0,4],j\in [0,2], k\in [0,1])$ の形で一意的に表されることが分かる■

以下語の定義を述べている.

prop. n変数の長さmの語 $x_{i_1}^\pm x_{i_2}^\pm \cdots x_{i_m}^\pm$ を決めることと, 写像 $\{1,\ldots,m\}\rightarrow \{1,\ldots,n\}\times \{1,-1\}$ を決めることは同値である.
pf. 最初の定義で表される集合をU, 後の定義の写像全体の集合をVとおき, これらが同等であることを示せば良い. Uはm=1なら $1\leq i_1\leq n$ だから, 符号(指数)の部分も考えて2n個の自由度がある. 語の添字に重複は許されるので, mが一般の場合では, $2n\times 2n\times \cdots \times 2n=(2n)^m$ 個の自由度がある. またVは写像の個数の公式により, $(2n)^m$ 個の写像があるので集合の濃度は一致する. つまり ${\rm card}U={\rm card}V=(2n)^m$ だから同等である■

n変数m長の語の集合を $W_{n,m}$ と書き, 長さ0のただ一つの元1が存在し, $x_ix_i^{-1}=x_i^{-1}x_i=1\ (\forall 1\leq i\leq n)$ とする(縮約をとるという). そうすると,

$W_n = \bigsqcup_{i=0}^\infty W_{n,i}$

を自由群と言う. これは実際積を語を連結させることに対応させて群を成すことが分かる. $1\in W_{n,0}\subset W_n$ は単位元である. 語の定義から $x_{i_1}x_{i_2}\cdots x_{i_k}\in W_{n,k}\subset W_n$ なら $x_{i_k}^{-1}x_{i_{k-1}}^{-1}\cdots x_{i_1}^{-1}\in W_{n,k}\subset W_n$ で, これは逆元である. 結合律は明らかだし, 演算が閉じていることは, 有限長の語の連結が高々可算長の語しか生成しないことから分かる(縮約によって割った商集合に積を定義しているが, これがWell-Definedなことの証明は略).

◇可解群と冪零群の基本性質

◇Sylow-p群の基本性質

(i) Sylow-p群の存在

(ii) Sylow-p群は互いに共役/p群を含むSylow-p群が取れる

(iii) Sylow-p群の個数は

コメントする

(iii) Sylow-p群の個数は $1\mod p$