可換環6 – 解析タネル

一段落したのでちょこちょこと書きためていたものを公開.

prob.1. Aをnoether ring, MをA上の有限生成加群とすると, MはネータA-加群である.
$M=\sum_{i=1}^n Ax_i$ と書けるので, 写像 $A^n\rightarrow M$ を $(a_1,\ldots,a_n)\mapsto \sum_{i=1}^n a_ix_i$ と作ると,
これは明らかにA-全準同型で, ${\rm ker} = \prod_{i=1}^n(0:x_i)$ だから,

$M\cong A^n/\prod_{i=1}^n(0:x_i)$

である. 完全列

$0\rightarrow \prod_{i=1}^n(0:x_i)\rightarrow A^n\rightarrow M\rightarrow 0$

において $A^n$ Noetherian⇔ $\prod_{i=1}^n(0:x_i),\ M$ はNoetherian■

prob.2-1. Mをneither A-Module, $u:M\rightarrow M$ をA-homとする. uが全射なら, uは同型である.

$u^n = \overbrace{u\circ \ldots \circ u}^n$ は一般のhomとして ${\rm Im}u^n\subset {\rm Im}u^{n-1}$ だから, Mの部分A-Moduleとしての増大列

${\rm ker}u\subset \ldots \subset {\rm ker}u^n \subset \ldots$

が取れる. MはNoetherianなので十分大きいnに対して ${\rm ker}u^n={\rm ker}u^{n+1}$ を満たす. $u^n\ (\forall n)$ はMへの全射で

$M/{\rm ker}u\supset \ldots \supset M/{\rm ker}u^n = M/{\rm ker}u^{n+1} \cong M$

よって ${\rm ker}u^n = 0\ (\forall n)$ ■

prob.2-2. MをArtinian A-Module, $u:M\rightarrow M$ をA-homとする. uが単射なら, uは同型である.

Mの部分A-Moduleとしての減小列

${\rm Im}u\supset \ldots \supset {\rm Im}u^n \supset \ldots$

に対し, 十分大きいnに対しMのArtin性から ${\rm Im}u^n={\rm Im}u^{n+1}$ となる. $u^n\ (\forall n)$ は単射なのでこれはMに同型で, 増大列

${\rm Coker}u\subset \ldots \subset {\rm Coker}u^n = {\rm Coker}u^{n+1} \cong 0$

が取れる. 故にuは全射となり, 同型■

prob.3. MをA-moduleとし, $N_i\ (i=1,2)$ をMの部分A-moduleとする. $M/N_i\ (i=1,2)$ がNoetherian A-Moduleなら $M/(N_1\cap N_2)$ もそうである.

0でない元 $x\in M/(N_1\cap N_2)$ を

$x=a_0x'+a_1x_1+a_2x_2\ (a_i\in A,\ x'\in M\backslash(N_1\cup N_2),\ x_i\in N_i\backslash N_j\ (i\neq j))$

と書くとき, 写像 $x\mapsto a_0x' + a_2x_2\in M/N_1$ は $M/N_1$ へのwell-definedな上へのA-homになる. これによる完全列

$0\rightarrow N_i/(N_1\cap N_2)\cong (N_1+N_2)/N_j\rightarrow M/(N_1\cap N_2) \rightarrow M/N_i\rightarrow 0\ (i=1,2,\ i\neq j)$

を考えると, $(N_1+N_2)/N_j\subset M/N_j$ はNoetherian A-moduleの部分A-ModuleだからNoetherian, よって拡大 $M/(N_1\cap N_2)$ もNoetherian. NoetherianをArtinianに変えても成立する■

prob.4. MをNoetherian A-moduleとし, aをAにおけるMの零化イデアルとする. このときA/aはNoetherian ringである.

Mの部分A-moduleの増大列 $\{M_i\}_i\ (M_n=M_{n+1})$ をとっておき, $M_i$ の零化イデアルを $a_i = (0:M_i)$ と置くと, これはAのイデアルの停留的な減少列

$a_1\supset a_2\supset \ldots \supset a_n = a$

を成す. 逆にaを含むAの任意のイデアルの減少列 $\{a_i\}_i$ に対し, $a_i$ で零化されるMの元の集合 $(0:a_i)_M=M_i$ はMの部分A-Moduleであるから, 上と同様にMの停留的な部分A-Moduleの増大列を取れる. aを含むAのイデアルと $A/a$ のイデアルとは一対一対応があるから, A/aはNoetherian ringである■

prob.5. Aを環Bの部分環とし, 集合 $B-A$ が乗法的であるとする. このときAはBにおいて整閉である.

$x\in B\backslash A$ がA上整なら, 整従属を示す方程式から

$x(x^{n-1}+a_1x^{n-2}+\ldots+a_{n-1})=-a_n\in A$

を得る. $x\in B\backslash A$ なら, $x^{n-1}+a_1x^{n-2}+\ldots+a_{n-1}\notin B\backslash A$ . つまり $x^{n-1}+a_1x^{n-2}+\ldots+a_{n-1}=a\in A$ だが, これはnの最小性に反す■

prob.6-1. Aを整域Bの部分環とし, CをBにおけるAの整閉包とする. f,gを $B[x]$ のモニック多項式とし, $fg\in C[x]$ を満たすとする. このとき, $f,g\in C[x]$ .

Bを含むfgの最小分解体をLとすると, $f=\prod_j(x-\mu_j),\ g=\prod_j(x-\eta_j)\ (\mu_j,\eta_j\in L)$ と分解する. $\mu_j,\eta_j$ は共にC上のモニック多項式fgの根で, 従ってC上整. $\mu_j,\eta_j$ はそれぞれf,gの根でもあり, C上整であるLの元はLの部分環を成すから, f,gの係数はC上整. 仮定よりf,gの係数はBの元で, BにおけるCの整閉包をDとすると, 整従属の推移律によってDはA上整. よって $C=D$ だから, $f,g\in C[x]$ ■

prob.6-2. B(or A)が整域であるという仮定なしに6-1が成り立つ.

Aが整域でなければその拡大環であるBもまた整域でないので, Aが整域でないと仮定して6-1を示す.
hom $C\rightarrow B$ による $q\in {\rm Spec}(B)$ の縮約 $q^c=q\cap C$ はCの素イデアルで, その剰余環 $C/q^c$ 上の多項式を考える.

射影 $C[x]\ni f(x)g(x)\mapsto \overline{f(x)g(x)}=f(x)g(x)\mod q^c[x]$ を通じて, $C/q^c$ は $A/A\cap q$ 上整. $\overline{f},\ \overline{g}$ は, 整域 $B/q$ 上の多項式として, 6-1より $C/q^c[x]$ の元である. よって $\overline{f},\ \overline{g}$ の係数は $A/A\cap q$ 上整.

prop.7.1 Aがネータ環で ${\rm dim}A=0$ であることは, Aがアルチン環であるための必要十分条件である.
(必要性) アルチン環の全ての素イデアルは極大であるから, ${\rm dim}A=0$ . またアルチン環の極大イデアルは有限個で, それらを $\{m_j\}_{j\leq n}$ とすると, 冪零元根基:

$\prod_j m_j = \mathfrak{N}$

はアルチン環の性質からイデアルとして冪零である. そこで $\mathfrak{N}^k=0$ なる最小のkに対し,

$\prod_j m_j^k\subset (\cap_j m_j)^k = \mathfrak{N}^k = 0$

※可換環において, イデアルの冪に関する可換性 $\prod_j m_j^k = (\prod_j m_j)^k$ が成立することに注意.

が成立する. 零イデアルが極大イデアルの積で表される時, アルチン環であることとネータ環であることは同値であるから, AはNoetherianである■

(十分性) 零イデアルは準素分解を持ち, 対応する有限個の孤立素イデアル $m_1,\ldots,m_n$ に対し, 冪零元根基は $\mathfrak{N}=\cap_j^n m_j$ で表される. ${\rm dim}A=0$ より, $m_j$ は極大で, ネータ環の冪零元根基もイデアルとして冪零であるから, $\mathfrak{N}^k=0$ . 故に必要性を示したときと同様にして, $\prod_j^n m_j^k=0$ を得る. 零イデアルが極大イデアルの積として表されたので, これはアルチン環である■

lemma.1. 相異なる極大イデアル $m_1,\ldots,m_n$ は互いに素である.
同値な命題「 $A\rightarrow \prod_j^n A/m_j$ が全射である」を示す. それには

$\exists a\in A,\ a\equiv 1\mod m_1\equiv 0\mod m_j\ (j>1)$

を示せば十分である. $\nu = \cap_{j=2}^n m_j$ に対し, $\nu \backslash m_1$ は空でない(Aの単元全体の集合Sによる商環を考えると, $m_j$ はSと交わりを持たない. よって $r(m_j)=m_j,\ \nu^{ec}=\nu$ であり, 前式は $\nu$ の相異なる極大イデアルによる最短の準素分解を与えていることから従う).
$a\in \nu \backslash m_1$ をとると, aは体 $A/m_1$ で単元なので, ある $b\in A\backslash m_1$ が存在し, $ab\equiv 1\mod m_1$ . $\nu$ はイデアルなので $ab\in\nu$ . これは求める性質を持つ■

ex.5.27. 体Kに対し, ∑をKのすべての局所部分環の集合とする. この集合に次のようにして順序を入れる. すなわちA, Bを∑に入っている二つの局所環とするとき,

$A\leq B\Leftrightarrow A\subset B \wedge rad(A)=rad(B)\cap A$

と定義する(B dominates A). このとき∑には極大元が存在し, $A\in \Sigma$ が極大であることと, AがKの付値環であることは同値である(※ここでradはヤコブソン根基だが, 局所環なのでそれはただ一つの極大イデアルである).

pf. まず $K\in \Sigma$ である(体K自身極大イデアル(0)を持つ局所環である)から∑は空ではない. ∑から取った全順序部分集合族の鎖の和を, $\cup A_j=A$ とする. これは1, 0を含み和と積について閉じていて $A\subset K$ であるからKの部分環である. $A=A_j$ となるものがあるからこれは局所環であり, $A\in\Sigma$ .

(A,m)が∑の一つの極大元とする(mはAの極大イデアル). $x\in K\backslash\{0\}$ に対し, Kの中でA上生成される部分環 $A[x]\subset K$ を考える. Aが局所環なので, $m[x]\neq A[x]$ か $m[1/x]\neq A[1/x]$ 少なくとも一方は成り立つ. $m[x]\neq A[x]$ を仮定すると, $A[x]$ の極大イデアルで $n\supset m[x]$ を満たすものがある. その縮約は $n^c=A\cap n=m$ である. 実際nはmを含む真のイデアルであるから, Aにおいてmに対応する. $A[x]_n$ はAを含み, $nA[x]_n$ を極大イデアルとして持つKの局所部分環で,

$m\subset n\subset nA[x]_n$

を満たす. 同様にして $nA[x]_n$ がnを含む真のイデアルであることから, $A\cap A[x]_n=A$ . ∴ $A[x]_n$ はAを支配する. Aの極大性から $A=A[x]_n$ . よって最初に取った零でないKの元xはAに含まれるので, AはVR.

逆にAがKのVRで(B,n)がAを支配するとする. $x\in B\backslash A$ に対し, $1/x\in A$ . $1/x$ はAで単元でないので, Aの極大イデアル $m=n^c$ に含まれる. よって $1/x\in m\subset n$ だが, これによりxはBで単元になる. これは矛盾である( $1/x\in n$ とし, 極大イデアルが単元を含む)■

ex.5.31. 全順序可換群 $\Gamma$ に値を持つ体Kの付値を $\nu:K^*\rightarrow \Gamma$ とする. このとき $A=\{x\in K^*|\nu(x)\geq 0\}\cup \{0\}$ はKの付値環である.

p.f. $x,y\in A$ とする. $\nu(xy)=\nu(x)+\nu(y)\geq 0$ より $xy\in A$ . また $\nu(x+y)\geq \min{\nu(x),\nu(y)}\geq 0$ より $x+y\in A$ . $\nu(1)=\nu(1\cdot 1)=\nu(1)+\nu(1)$ だから $\nu(1)=0$ . よって $1\in A$ .

これによりAは環である.

$x\in K^*$ に対し, $0=\nu(1)=\nu(xx^{-1})=\nu(x)+\nu(x^{-1})$ であるから, $\nu(x)\geq 0\vee \nu(x^{-1})\geq 0 \Leftrightarrow x\in A\vee x^{-1}\in A$ .

これによりAは付値環である■

prop. 9.0.1 整域A, 商体K, 離散付値νがあるとする. AがKのDVRであるとき, その極大イデアルmは0か $\nu(x)>0$ を満たす $K^*$ の元である.

DVRは局所環であるから, $\nu(x)=0\ (x\in K^*)\Leftrightarrow x\in A^*$ を示せば十分である. $x\in A\backslash A^*\cup \{0\}$ とする. AはDVRだから $1/x\notin A$ として良い. このとき $0=\nu(xx^{-1})=\nu(x)+\nu(x^{-1})$ だが, $\nu(x)>0$ だから $\nu(x^{-1})=-\nu(x)<0$ . よって $\nu(x)\neq 0$ . 逆に $x\in A^*$ なら $\nu(x^{-1})\geq 0,\ \nu(x^{-1})\geq 0$ で, 上の等式から $\nu(x)=0$ である他ない■

prop. 9.0.2 (A,ν)が商体KのDVRで, Aの任意の非零イデアルをαとする. 適当な $x\in \alpha$ に対しその値 $\nu(x)\in Z$ は最小値を持つ.

αが単位イデアルであれば, 定義から0が最小値である(Aの単元に対応する). αが零でない真のイデアルと仮定すると, $x\in\alpha$ は単元ではないから $\nu(x)>0$ ( $x\in A\Leftrightarrow \nu(x)\geq 0$ を忘れないこと). よって最小値が存在する■

$0<g=\min{\nu(\alpha)}=\nu(x)$ となる $x\in\alpha$ を固定する. 付値は仮定よりZへの全射だから, $\nu(a)=1$ となる $a\in A$ がある. よってそのようなa,xに対し, $\{\nu(a^kx) | k\geq 0\}$ はg以上の全ての整数を含む. 従ってDVRの任意の非零イデアルαは, 適当な非負整数gに対し, $m_g = \{\nu(x)\geq g | x\in K^*\}$ と表される集合と一致する.

$m=m_1\supset m_2\supset \ldots$

が唯一のイデアルの鎖であり, AはNoetherianである.

上でとったように $\nu(x)=1$ を満たす $x\in A$ に対し, $(x)=m_1=m$ . 特に $(x^g)=m_g\ g\geq 1$ だから, Aの全ての非零イデアルはxの冪で生成される. 従ってAの非零素イデアルはmのみで, DVRは次元1のネータ局所整域と分かる.

逆にAを次元1のネータ局所整域とするとき, 同値な性質について次のようなものがある.

prop. 9.2

mを極大イデアル, k=A/mとする.

AはDVR
Aは整閉
mは単項イデアル
${\rm dim}_k(m/m^2)=1$
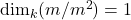
すべての非零イデアルはmの冪
Aのある元xが存在し, すべての非零イデアルは 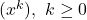$(x^k),\ k\geq 0$ という形をしている

(1)⇒(2) VRの性質として, $x\in A\vee x^{-1}\in A\ (\forall x\in K)$ がある. $x\in K\backslash 0$ をA上整とすると,

$x^n+a_1x^{n-1}+\ldots+a_n = 0\ (a_i\in A) \ \cdots\ (*)$

を満たす $\{a_i\},n$ がある. $x\in A$ なら何も証明することは無いので, $x\notin A$ とすれば, $x^{-1}\in A$ . $x^{n-1}$ を(*)に掛けて

$x = -(a_1+x^{-1}a_2+\ldots+x^{n-1}a_n)\in A$

これは矛盾である.

(2)⇒(3)

(A) αが非自明なイデアル(0,Aと異なるイデアル)ならばm-準素イデアルで, $\alpha\supset m^n$ となるnが存在する. 実際Aは次元1の局所環であるから0以外の唯一つの素イデアルmは極大で, $r(\alpha)=m$ となる(αの根基はαを含む素イデアルの共通部である). mが極大だからこれはαがm-準素イデアルであることを意味し, ネータ環の任意のイデアルは根基のある冪を含むから, $m^n\subset \alpha$ となるnを取れる(α=0のとき $m^n=0$ となるnが存在しなくてはいけないが, これはAがアルチン局所環であることを要求するのでこの場合は省く).

$a\in m\backslash 0$ なら, (A)より $m^n\subseteq (a)\wedge m^{n-1}\nsubseteq (a)$ となるnを取れる. そこで $b\in m^{n-1}\backslash (a)$ なるbが存在する. $x=a/b\in K$ に対し, $x^{-1}=b/a\in A$ なら $b/a=a'/1\ (\exists a'\in A)$ だから $s(aa'-b)=0$ . Aは整域だからこれは $b=aa'$ を意味し, $b\notin (a)$ に反する. よって $x^{-1}\notin A$ . Aは整閉だから, $x^{-1}$ はA上整でない. Aはネータ環だから, mはA加群として有限生成で, $x^{-1}m$ は $A[x^{-1}]$ 加群として忠実(Aが整域なので $A[x^{-1}]$ も整域である). 従って $x^{-1}m\subseteq m$ なら中山の補題により $x^{-1}$ がA上整となり, 矛盾. よって $x^{-1}m\nsubseteq m$ . 一方xの作り方から $x^{-1}m\subseteq A$ である( $x^{-1}m\ni (aa')/a=a'\in A\ (\exists a'\in A)$ ). よって $x^{-1}m$ は単元を含み,

$x^{-1}m = A \Leftrightarrow m=(x)$

(3)⇒(4) 極大イデアルmのA加群としてのある生成系(今Aがネータ環だから有限)は, (A加群の)準同型 $m\rightarrow m/m^2$ で写った像により $m/m^2$ のkベクトル空間としての基底を成す. 今mは単項イデアルを仮定しているから, A加群として唯一つの元で生成される. よって ${\rm dim}_k(m/m^2)\leq 1$ . 一方 $m\neq m^2$ より ${\rm dim}_k(m/m^2)=1$ (ネータ局所環において, $m^n\neq m^{n+1}\ (\forall n)$ か, $m^n=0\ (\exists n)$ いずれか一方のみがおこる. 後者の場合アルチン局所環となり, 次元は0になるので仮定に反する).

(4)⇒(5) (A)により任意の非零イデアルαに対し, $\alpha\supseteq m^n$ となるnがある. ネータ局所環がアルチン局所環であることと, $m^n=0$ となるnがあることは同値であるから, 剰余環 $B=A/m^n$ はアルチン局所環になる. 同型 $m/m^2\cong (m/m^n)/(m^2/m^n)$ があるから, ${\rm dim}_k(\overline{m}/\overline{m}^2)={\rm dim}_k(m/m^2) = 1$ . これはアルチン局所環Bにおいて, 全てのイデアルが単項イデアルであることを意味する(Atiyah, 8.8). $m=(x)$ に対し, $m^n=(x^n)\subseteq \alpha=(y)\subseteq m=(x)$ とすると, Bにおいて極大イデアルはただ一つ一意的に存在するから $y=x^k\ (1\leq k\leq n)$ となる.

(5)⇒(6) $m\neq m^2$ より $x\in m\backslash m^2$ がある. 仮定より $(x)=m^r$ だが, $r\geq 2$ だとxの取り方に矛盾する. よってr=1. ∴すべてのイデアルαは $\alpha = (x^k)=m^k\ (k\geq 0)$ と書ける.

(6)⇒(1) VRの構成に寄る.