中学の新課程内容で気になったこと等

指導要領の改変により, 中3以降の数学に「同値類への分類」,「ユークリッドの互除法」といった群論の概念を踏襲するものが出てきました. それで驚くことがあります. ガロア200周年も関係しているのでしょうか. 今日は中三の新課程の問題で目を引いたものを見つけたので紹介します. なお, その際群の表現を使うことで一般的な説明になるよう努力したいと思います.

[問題]

6つの電球が点灯せずに並んでいる.
サイコロを2度振って, 1度目に出た数をp, 2度目に出た数をqとする.
このとき左からp個までの電球を点灯し, その後右からq個までの電球を点灯する.
※例えば(p,q)=(4,3)のときは ○○○●○○ という風に点灯する.

(1) 左3つ, 右1つが点灯している場合の数を求めよ

すぐに思いつくやり方としては, 次のような解法が考えられると思います.
(i) 左a個, 右b個が点灯している場合の(p,q)の組全体からなる集合を(p,q)の関数で表現する(この集合を $K_{a,b}$ と書くことにします)
(ii) n個が点灯している(p,q)の組全体からなる集合を(p,q)の関数で(この集合を $L_n$ と書くことにします)

考察を加えると…
p+qが5を超えない場合, つまりp+q≦5であれば, (i)において(a,b)=(p,q)が成り立ち, (ii)においてp+q=nである.
またp+q=6または12であれば, (i)においてそれぞれ(a,b)=(6,6), (a,b)=(0,0), (ii)において6, 0.
7≦p+q≦11のときはp+q mod 6=rとおいて, (i)において (a,b)=(p-r,q-r), (ii)において n=p+q-2r.

これらを踏まえて $K_{a,b}, L_n$ を集合で表現すると次のようになるでしょう.

$D=\{n\in \mathbb{N}| 1\leq n\leq 6\}, r=(p+q) mod 6)$ とおいて,
$K_{a,b}=\Big\{(p,q)\in D^2|f_{a,b}=0 \Big\}$
$\quad s.t.\quad f_{a,b}(p,q)=\Bigg\{ \begin{array}{l} (a-p,b-q)\quad (p+q\leq 5) \\ (a-6,b-6),(a,b)\quad (p+q=6,12) \\ (a-p+r,b-q+r)\quad (7\leq p+q\leq 11 \end{array}\qquad \forall (p,q)\in D^2$

$L_n=\Big\{(p,q)\in D^2| g_n=0\Big\}$
$\quad s.t.\quad g_n(p,q)=\Bigg\{ \begin{array}{l} p+q-n\quad (p+q\leq 5) \\ 6-n, n\quad (p+q=6,12) \\ p+q-n-2r \quad (7\leq p+q\leq 11) \end{array} \qquad \forall (p,q)\in D^2$

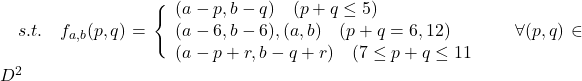
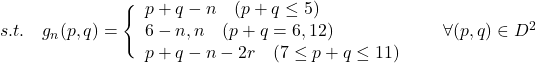
こうして集合で表現してみれば, (1)は次の命題(1)’と等価になるのです.

(1)’ $K_{3,1}$ の位数を求めよ

解. $K_{3,1}\ni (3,1), (5,3)$ の二つ.

応用として4つ点灯していて $K_{3,1}$ に含まれないような場合の数を考えることができます. そのような集合は $L_4^*=L_4-K_{3,1}=\{(p,q)|f_{3,1}(p,q)\neq 0 \wedge g_4(p,q)=0 ; \forall (p,q)\in D^2\}$ と表され, 簡単な計算で(1,3),(2,2),(6,2),(2,6)が順次求まります.

(1)の結果を使わずに一般的な演算で $(6,2),(2,6)$ を求める場合, $g_n$ の3つ目の式から $p+q-2r=4$ を考えなくてはいけません. 次のようにします.
$p\geq q$ として( $p<q$ の時はpをqと入れ替えて考えれば良い), $p=qk+r\quad (k=1,2)$ とおけば, $p=(2k+1)q-4$ から $(3q-4, q), (5q-4, q)\quad (7\leq p+q \leq 11).$ これを満たすようなものは順にq=3, 2しかないので (5,3),(6,2)が出ますが, $f_{3,1}(5,3)\in K_{3,1}$ から(5,3)は省かれ, (p,q)入れ替えたものも含めて上記結果.

$\mathbb{Z}^4$ の部分空間 $\mathbb{Z}_6^4=\{(p,q,a,b)\}$ を, $D^2\otimes D^2=\{m(p,a)\times n(q,b)\}\ni (x,y)$ とx,y平面に射影すると, z軸に $f_{a,b}$ の値をとって次のようなグラフを描けます. z=0を表すチェック柄の平面と, 蛇のようにうねる曲面( $=f_{a,b}$ )との交点( $\in K_{a,b}$ )を見れば, 規則性を持って $Kerf_{a,b}$ が点在している様子が分かります.

数学の奥深いところは, それが例え小学校の算数であろうと侮れないところですね.
数学の全ての分野は有機的にそして密に繋がっており, 見方を変えれば非常に複雑にも, 単純にもなるのでした.