睡眠を・・

朝になって眠る. 駄目だなぁと思ってるが.

——————————–

Tunnell’s Theoremにおける次の二条件を考える.

nは平方因子を持たない正の奇数として,

[A] nは合同数
[B] $latex t(x,y,z)=2x^2+y^2++8z^2=n$を満たす整数の3つ組(x,y,z)の数は, $latex t(x,y,2z)=n$を満たす整数の3つ組(x,y,z)の数の2倍に等しい.

【命題】
条件[B]は次と同値.

[B]’ nを$latex t(x,y,z)=2x^2+y^2++8z^2$(x,y,z∈Z; zは奇数)という形で表す方法の数と, nをt(x,y,z) (zは偶数)の形で表す方法の数が等しい.

【証明】
[B]⇒[B]’
t(x,y,z)の対称性と非負値性から $latex {\rm A}_n(z\in \mathbb{Z}/2\mathbb{Z})=\{(x,y,z)\in (\mathbb{Z}^+)^2\times \mathbb{Z}/2\mathbb{Z}|n=t(x,y,z)\}$とおき, A_n(z)の個数を問題とすれば十分($latex \mathbb{Z}^+$は非負整数).

#A_n(z)=#A_n(0)+#A_n(1)
であることと
#A_n(z)=2#A_n(2z)
であることから, 直ちに
#A_n(1)=2#A_n(2z)-#A_n(0).

zは任意に与えられて2zが$latex 2\mathbb{Z}$内を動くから, #A_n(2z)=#A_n(0). [B]’⇒[B]も同様の証明が通用する■

————————————————–
Abel群の帰納的極限の表示を直感的には理解できなかったので, 少し検証してみました.

帰納系{M_λ,f_λμ}がR加群の族として通常通り与えられているものとして, 半順序集合Λを簡単に

$latex \Lambda=\mathbb{N}$

とおけば全順序となる. λ≦μ∈Nに対して $latex f_{\lambda \mu}(ax_\lambda + y_\lambda)=ax_\mu + y_\mu (a \in {\rm R}, x_\lambda \in M_\lambda, x_\mu \in M_\mu)$と置けば, 帰納系の仮定を満たす.

$latex U=\bigoplus_{\lambda\in \Lambda}M_\lambda$の部分(直和)加群Xを,

$latex X=\Big\{\upsilon_\lambda(x_\lambda)-\upsilon_\mu(f_{\lambda\mu}(x_\lambda))\in U|\lambda \leq \mu \in \Lambda, x_\lambda \in M_\lambda \Big\}$
と定義する(ただしυ_λはM_λ→Uへの埋入写像である).
帰納的極限の定義から, R上このXが生成する部分加群の形が見れればOK.

Xの基底として, $latex \begin{pmatrix} 1_{M_1} \\ -1_{M_2} \\ {\bf 0} \end{pmatrix}, \begin{pmatrix} 1_{M_1} \\ {\bf 0} \\ -1_{M_3}\end{pmatrix}, \begin{pmatrix} {\bf 0} \\ 1_{M_1} \\ -1_{M_2} \end{pmatrix},\ldots$なるものが取れる(太い0は以下全ての要素0を表す). 今添字集合Λは自然数であるから可算無限だが, 直和の定義から一般に, n個の要素を除いて0であるような族だけを問題にできる. そのような基底の和で全ての要素が1であるもの(帰納的極限$latex \lim_{\rightarrow} M_\lambda$の加群としての単位元で, これを1_Uと記す)を表せるかは, 次の方程式系が自明でない解を持つことと同等.

$latex \begin{pmatrix} 1 & 1 & \ldots & 1 & 0 & \ldots & 0 & 1\\ -1 & 0 & \ldots & 0 & 1 & \ldots & 0 & 1\\ 0 & -1 & \ldots & 0 & -1 & \ldots & 0 & 1 \\ &&&\ddots \\ 0 & 0 & \ldots & 0 & 0 & \ldots & 1 & 1 \\ 0 & 0 & \ldots & -1 & 0 & \ldots & -1 & 1 \end{pmatrix}{\bf x}={\bf 0}$

すぐに分かるが自明でない解はない. つまり$latex 1_U\notin $. よって任意のλ∈Λに対して$latex 1_{M_\lambda}$は次の可換図式を追えば分かるように, 同じ類に属している.

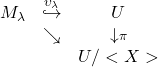
しかしなんでΛが有向集合だと, あるλ∈Λとあるx_λ∈M_λで, lim M_λ∋x=f_{λ∞}(x_λ)と表すことができるのだろう・・・.

—————–訳注—————————–
$latex {}^1$ この表記は計算に便利だと思うので説明しておきます. R=Z_8 (8を法とした剰余加群)をZ上の環と見做すと, pZ (pは8と互いに素)は標数pを持つ単位イデアルとなるので, Rのイデアルが真にRに含まれるには pが8の約数であることが必要十分. なので8と互いに素なZ_8の元からなる集合, すなわち{1,3,5,7}=Cの部分集合でx∈Z_8のn乗数となるもの全体をC_nとすると, 次のような関係が見られる.

$latex {\rm C}_n=\Bigg\{ \begin{array}{l} C \quad (n=2k+1) \\ \{1\} \quad (n=2k) \end{array}$