可換環5 – icefog BLOG

Googleのロゴが

生誕後200年になるGeorge Booleにちなんだものになってていいですね♪
40歳に満たず病死してしまったのですが, 代数・解析の各方面で著名な結果を残しています. そういえばBooleの生まれた時期はChopinやLiszt, R. Schumannなどのロマン派の作曲者が全盛だった時期と重なりますな.

今回はBooleへの敬意を表し, Booleの残したBoolean Algebra (ブール代数)を紹介しようと思います.

Def. 半順序集合Lが束(lattice)であるとは, Lにおける２項演算 $\vee,\ \wedge$ が束の公理AAE(associative(結合律), absorption(吸収律), exchange(交換律))を満たすことを言う. すなわち $\vee$ の場合のみ書くと( $\wedge$ も同様)任意の $a,b,c\in L$ に対し,

(las) $(a\vee b)\vee c=a\vee (b\vee c)$
(lab) $a\vee(a\wedge b)=a$
(lex) $a\vee b=b\vee a$

を満たすことを言う.

束に更にBCD条件(bounded(有界性), complemented(可補性), distributive(分配律))を付け加えたものをBoolean lattice (またはBoolean algebra)という.

(lbo) $\displaystyle{\bigvee_{x\in L} x = 1\in L,\ \bigwedge_{x\in L}x=0\in L}$
(lco) $\forall a\in L,\ uniquely\ \exists \neg{a}\in L,\ a\vee\neg{a}=1,\ a\wedge\neg{a}=0$
(lde) $a\wedge (b\vee c) = (a\wedge b)\vee (a\wedge c)$

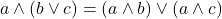
Lをブール束とすると, Lにおける加法と乗法を次の式によって定義することでブール環A(L)が得られる.

$a+b=(a\wedge \neg{b})\vee(\neg{a}\wedge b),\ ab=a\wedge b$

実際Lは $-a=a\in L,\ 0=a+a\in L$ によって加法と束演算に整合性があることが分かる(閉性, 可換性, 結合律は明らか).
分配律を示すのに, A(L)ではde Morgan Lawが成り立つことを見る.

$\begin{array}{lcl} 0 &=& (a\wedge b)\cdot \neg{(a\wedge b)} \\ &=& a\cdot \neg{a} \cdot b \cdot \neg{b} \\ &=& (a\cdot \neg{b})\wedge (b\cdot \neg{a}) \\ &=& a(\neg{a}\vee \neg{b})\wedge b(\neg{a}\vee \neg{b}) \\ &=& (a\wedge b)(\neg{a}\vee \neg{b}) \end{array}$

$a\wedge b$ の取り方は任意で可換だから, $\vee$ の場合も同様にして, 一般に

$\begin{cases} \neg{(a\wedge b)} =& \neg{a}\vee \neg{b} \\ \neg{(a\vee b)} =& \neg{a}\wedge \neg{b} \end{cases}$

が成り立つ(しかしこの時点では和とde Morgan Lawとの整合性を見ていない). また,

$\begin{array}{lcl} 1 &=& \neg{0} \\ &=& \neg(a\neg{a}) \\ &=& \neg{a}\vee \neg\neg{a} \\ 0 &=& \neg{1} \\ &=& \neg(a\vee \neg{a}) \\ &=& \neg{a}\wedge \neg\neg{a} \end{array}$

から,

$\neg\neg a = a$

も分かる. これにより

$\begin{array}{lcl} (a\wedge b) + (a'\vee b') &=& (a\wedge b)\cdot \neg(\neg a \vee \neg b) \vee (\neg a \vee \neg b)\cdot \neg(a\wedge b) \\ &=& (a\wedge b)^2 \vee (\neg a \vee \neg b)^2 \\ &=& (a\wedge b) \vee (\neg a \vee \neg b) \\ &=& (a\wedge b) \vee \neg (a\wedge b) \\ &=& 1 \end{array}$

de Morgan Lawはブール代数と整合する. 以上から分配律が導かれる.

$\begin{array}{lcl} ab+ac &=& ab\cdot \neg(ac)\vee \neg(ab)ac \\ &=& ab(\neg{a}\vee \neg{c}) \vee ac(\neg{a}\vee \neg{b}) \\ &=& ab\neg{c} \vee a\neg{b}c \\ &=& a(b\neg{c} \vee \neg{b}c) \\ &=& a(b+c) \end{array}$

逆にAをブール代数とすると, 半順序

$a\leg b \Leftrightarrow a=ab$

によって $(A,\leg)$ はブール束を成すことが示される.

a,bの上界の集合をHとおくと, $H=\{c\in A|ac=a,bc=b\}$ で, $1\in H$ . 計算により, aの積により不変であるブール代数Aの元は

$a+\sum_i (x_i+ax_i)$

の形しかありえないことが分かる. bの積についても同様に考えると, 2倍写像によって0に消えるから,

$\min{H}=\sup(a,b)=a\vee b=a+b+ab$ である. 同様の考察で, $a\wedge b=ab$ とおける. $\neg{a}=1-a$ とおくと, 可補性, 分配律, de Morgan Lawも満たすことが見れる. よってこれはBoolean Latticeになる.

Theorem(Stone). 任意のブール束は, あるコンパクト・ハウスドルフ空間の開かつ閉である部分集合の作る束に同型である.

pf. 上述のことにより, 与えられたブール束をLとすると, Lによって定まるブール環A(L)=Aが同型を除いて一意的に対応する. $Spec(A)=X$ はZariski Topology Spaceとしてコンパクト・ハウスドルフ空間である. そこで $(S(X),\leq)$ をXの冪集合族に包含順序を入れたものとすると, これは束になり( $(S(X),\cap,\cup)$ ),

$B=\{U\subset X | U^\circ = \overline{U}=U\}=\{X_f | f\in A\}$

はその部分束になる(開かつ閉な集合全体が集合演算で閉じているのは明らかであろう). また, $\emptyset,\ X\in B$ で, これらが最大・最小元を与える. 分配・結合律は集合演算の規則に準じるのでここでは述べない. 以上からBはブール代数になる.

$\phi: L\rightarrow B$

を写像とする.

任意の $f\in A$ に対し, $X_f$ はXで開かつ閉(当然Xは非連結位相空間である)で, しかもXにおいて開かつ閉である部分集合は $X_f$ の形の集合に限るので, $\phi(f)=X_f\in B$ によって全射. $X_f=\emptyset\Leftrightarrow f\ is\ nilpotent$ であるが, $f\in A$ はブール代数の性質から冪等で, 0以外の元は冪零に成り得ない. よって $\phi$ は単射. $\phi$ が順序単射であることを示せば, 順序同型, この場合束同型を構成できたことになる.

$f\leq g\Leftrightarrow f=fg \Rightarrow f\in (g)$ で, 逆に $f\in (g)$ なら $f=ga$ となる $a\in A$ があって, $fg=ga=f\Rightarrow f\leq g$ .

よって $f\leq g \Leftrightarrow f\in (g)$ . このとき $X_f=X_ga=X_g\cap X_a \subset X_g$ となるから,

$f\leq g\Rightarrow X_f\subset X_g$

は示された. 逆は

$\begin{array}{lcl} X_f\subset X_g &\Leftrightarrow & V((g))\subset V((f)) \\ &\Leftrightarrow & \forall p\in V((g)),\ p\in V((f)) \\ &\Leftrightarrow & (g)\subset p \Rightarrow (f)\subset p \\ &\Leftrightarrow & \forall p\in V((g)),\ \exists a\in A,\ ga=f\in p \\ &\Leftrightarrow & f\leq g \end{array}$

による■

$X\neq \emptyset$ が既約な位相空間であるとは, 全ての空でない開集合がXで稠密, つまり集合の作用子で書けば, $\forall O\in \mathfrak{D},\ \overline{O}^c=O^{ci}=\emptyset$ となり, 任意の開集合の補集合に含まれる開集合は空集合に限ることを言う. このとき

prop 19. $Spec(A)$ が既約 $\Leftrightarrow\ r_A(0)\in Spec(A)$
pf 19.

$\begin{array}{lcl} Spec(A)\ is\ irreducible &\Leftrightarrow& \forall X_f,\ X_g\ (f,g\notin r_A(0)),\ X_f\cap X_g\neq \emptyset \\ &\Leftrightarrow& X_{fg}\neq \emptyset \\ &\Leftrightarrow& fg\notin r_A(0) \\ &\Leftrightarrow& r_A(0)\in Spec(A) \qquad \blacksquare \end{array}$

prop 21.6. $\phi:A\rightarrow B,\ \psi:B\rightarrow C$ を環の準同型とすると, それらの合成は誘導されたSpectrumの間の写像の合成を誘導する. つまり次が成り立つ.

$(\psi\circ \phi)^*=\phi^*\circ \psi^*$

pf 21.6. A, B, CのSpectrumを順にX, Y, Zとする. 環の準同型の合成は環準同型で, そのcodomainにおける素イデアルの縮小イデアルは相変わらず素イデアルであるから, $(\psi\circ \phi)^*:Z\rightarrow X$ を誘導する. これらが同じ像に移るのは $\phi^*=\phi^{-1}|_Y,\ \psi^*=\psi^{-1}|_Z$ という定義から明らか■

prop 21.7. Aは唯一の0でない素イデアルpを持つ整域とし, KをAの商体とする. $B=(A/p)\times K$ とおく. 写像 $\phi:A\rightarrow B$ を $\phi(x)=(\overline{x},x)$ で定義する. このとき $\phi^*$ は同相でない全単射である.

pf 21.7. $\phi^*$ が全射であることと, X=Spec(A)が縮小イデアルから成ることは同値で, またそのことは $\forall q\in X,\ q^{ec}=q$ と同値である. Aは整域だから, q=(0)ならK上の値を見れば明らかに $q^{ec}=q$ を満たす. またq=pとした場合も, $\phi^{-1}((0,y))\subset p\ (y\in p)$ だから $q^{ec}=q$ である. よって $\phi^*$ は全射.
Kは体だから, 素イデアルは自明なもの, すなわち(0)のみ. A/pにおける素イデアルはpを含むAの素イデアルと一対一対応があり, それはA/a上(0)だけである. よって(有限因子から成る)直積環において, $p_i\times \prod_{j\neq i}R_j\ (p_i\in Spec(R_i))$ の形のものは素イデアルであるから,

$Spec(A)=\{\{(0)\},\{p\}\},\ Spec(B)=\{\{A/p\times 0\},\ \{0\times K\}\}$

特に

$\phi^*(\{A/p\times 0\})=\{(0)\},\ \phi^*(\{0\times K\})=\{p\}$

である( $\phi^*$ が全射であると分かった時点でSpec(B)は二つより多い元を持たないことが分かる). これで $\phi^*$ は全単射.
Spec(B)はdescrete. 実際

$\displaystyle{\{0\times K\}^\circ = \bigcup_{Y_g\subset \{0\times K\},\ g\notin \{0\times K\}} Y_g = \{0\times K\}}$

である. $\{A/p\times 0\}$ も同様.

一方 $\{p\}^\circ = \emptyset,\ \overline{\{p\}} = V(p)=\{p\}$ で, $\{p\}$ はSpec(A)で閉であるから, XとYはhomomorphicではあり得ない ■

prop 5.30. $A\subset K$ を体Kの付値環(単位的とする). $U=A^\times\subset K^\times$ は乗法部分群(可換体を考えているので, 乗法群は可換群である). $\Gamma = K^\times/U$ . $\mu,\ \eta\in \Gamma$ の代表元をそれぞれ $x, y\in K$ とする.

$xy^{-1}\in A\Leftrightarrow \mu \geq \eta$

で $\Gamma$ に順序を入れる. これは $\Gamma$ 上群構造と適合している全順序を定義している.

pf 5.30. $\mu \geq \mu$ は $xx^{-1}=1\in A$ , $\mu \geq \eta\wedge \eta \geq \zeta$ なら $xy^{-1},\ yz^{-1}\in A$ より $xy^{-1}yz^{-1}=xz^{-1}\in A$ から $\mu \geq \zeta$ が示せる. $\mu \geq \eta\wedge \eta \geq \mu$ とする. このとき $xy^{-1}\in A^\times=U$ だから, $xy^{-1}=1_\Gamma$ . 故にx=y. 比較可能性は明らか.

$x_1,\ x_2$ を $\mu$ の二つの代表元, $y_1,\ y_2$ を $\eta$ の二つの代表元とする. $\mu \geq \eta$ なら $x_iy_j^{-1}\in A\ (i,j=1,2)$ . 逆に適当な $i,j\in \{1,2\}$ に対し, $x_iy_j^{-1}\in A,\ x_iU\subset\mu,\ y_jU\subset\eta$ が成り立つとすると, $x_ix_k^{-1}=1_U$ なら $x_i\in x_kU$ だから, $x_i=x_ku$ なるuをとって, $x_kuy_j^{-1}\in A$ . 可換だから $x_ky_j^{-1}\in Au^{-1}=A$ . これら順序が代表元の取り方に依らないことも分かった.

最後に群演算との整合性を見よう. $\forall\omega\in\Gamma$ について, $\mu \geq \eta\Rightarrow \omega\mu \geq \omega\eta$ を示す. $\mu,\ \eta,\ \omega$ の代表元x, y, zを取っておく. $xy^{-1}\in A$ だから, $zx(zy)^{-1}=xy^{-1}\in A$ . 先に示したように, Uの元の余剰分は単元として無視してよいので, これも代表元の取り方依らない.