前回から少し時間が経ってしまったが, 5章のレヴューをしてみよう.
本章では, 誤差逆伝播法と呼ばれる計算アルゴリズムについて解説している. ここでは計算グラフ[1]関数 (operator) をvertex (書籍ではnodeと呼んでいる), 代入 (value assignment or calculation) を edge とする有向グラフ.を順に(左から右に)辿ることを順伝播, 逆に辿ることを逆伝播と呼び, 計算グラフで表現されたLoss Functionの逆伝播の実装アルゴリズムのことをこう呼んでいるようだ. 順伝播に関数の合成を対応させ, 逆伝播では関数の(合成の)微分, 即ち連鎖律に対応させている.
この意味は, (厳密に) 解析的な意味においての微分はコンピュータ上実現できないし, 数値微分による近似もまた非効率的であるから, (然るべきクラスの) 関数を係数とし, (各nodeにおける)パラメタを変数とする可微分関数 (しばしば有理関数)で表現される形式的微分であれば, 計算グラフを使って予め決定論的に実装計画を立てることも, 従って実装をすることもできるという主旨である.
計算グラフの例
次の例は, 計算グラフとは何かを知る上では良いだろうと思う.
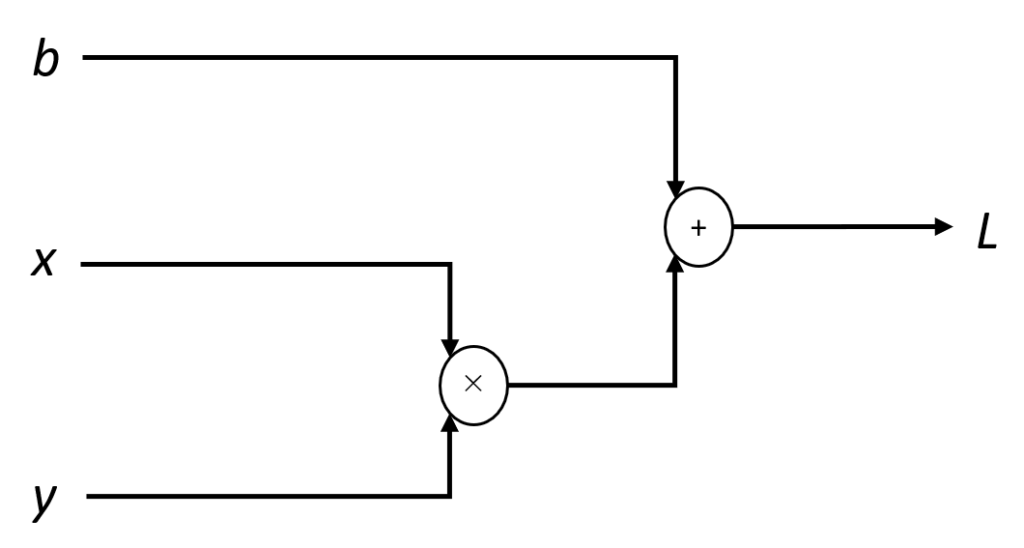
![]() の計算グラフの図.
の計算グラフの図.![]() の微小変位による寄与を, 各ノードにおいて, 各パラメタの高々多項式で表現するのが目標 (可能).
の微小変位による寄与を, 各ノードにおいて, 各パラメタの高々多項式で表現するのが目標 (可能). ![]() より右側または左側に他の計算があったとしても, それぞれの微分係数による寄与を適宜掛け合わせれば良い (連鎖律による).
より右側または左側に他の計算があったとしても, それぞれの微分係数による寄与を適宜掛け合わせれば良い (連鎖律による).
計算グラフは,
- 開平法
- 鶴亀算
- 連分数
等の例でみられる計算表現が本質であると思える. つまりLayer[2]幾つかのnodeとedgeをまとめて一つのnodeにしたもの.の構成を表す設計図である.
ここまででDeep Learningにおける計算グラフの有効性が十分説明されたとは言えない. 書籍内で幾つか挙げられているものをまとめると, 微分演算を効率的にかつシステマティックに行うことができる (*1)ということに集約されるだろう.
これは計算グラフの次の二つの性質による:
- 局所的な微分(係数)を張り合わせて(乗じて)全体へのパラメタの寄与を知ることができる (連鎖律)
- 計算(合成)の向き(順序)は順伝播で一度決めれば, 逆も決まる.
1により, Layerによる計算グラフのモジュール化ができることを, 2によりある特定のnodeにおける特定のパラメタの寄与を計算する際, 「どのLayerをどの順序で組み合わせるか」といった情報が自動的に決まってしまうことが分かる.
上記の例では1次元 (スカラー) 変数による演算とその微分を扱うのみであったが, より一般には (m, n)型関数行列の演算が含まれる. 最先端のNeural Network Modelでは数千億のパラメタを扱うそうだから, (*1) が重要であることは明らかと思われる.
補足
以下本章で幾つか補足した方が良いと思われた事柄について.
ベクトルの向きと転置について
NumPyでは, n次元ベクトルは常に行ベクトルで表され, その型 shapeは (n,) となる:
>>> x = np.array([0,1])
>>> x.shape #(2,)これは転置をしても同様:
>>> np.transpose(x).shape #(2,)(2行以上のnumpyArrayから成る) 行列を作った時は,
>>> W = np.array([[4,-1],[0,1],[-3,2]])
>>> W
array([[ 4, -1],
[ 0, 1],
[-3, 2]])
>>> W.shape # (3, 2)
>>> np.transpose(W).shape # (2, 3)とそのshapeは行, 列の順で表示される. この意味でn次元ベクトルのshapeは (1, n) であると期待されるのだけど, この場合は特別な扱いをしているので注意が必要.
行列の微分と型について
Affine Layerの逆伝播の計算において, 理論立ての省略が見られた. とりわけ著者は,
- 上流から (逆伝播で) 伝わってきた微分係数の型の説明を省略している (これは実装に重きを置いているので仕方がないかも知れない),
- 断りなく対象を同一視しているように見える,
ので, 以下で補足する. ここではNumPyの流儀に倣い全てのn次元ベクトルは行ベクトルとし, 実n次元空間を![]() と同一視して単に
と同一視して単に![]() と書く. また以下で説明するAffine Layerとして以下の計算グラフを使う.
と書く. また以下で説明するAffine Layerとして以下の計算グラフを使う.

Proposition.
に対し, Affine Transformation
を次で定める.
このとき出力の
における微分係数 (Jacobian) は次で表される.
Proof.
と書くと,
の第
成分は
よって
これより,
また,
最後の式は, (非自明な同一視により)次のように書ける.
よって連鎖律により求める式が成り立つ ■
実装
最後の約10ページは誤差逆伝播法の実装と勾配確認[3]数値微分と絶対差をepochごとに取って, 誤差逆伝播法の実装の正しさを評価すること.に充てられる. 「行列の微分と型について」で出力 (層) の記号で![]() を使っていたが, こはLoss Functionの
を使っていたが, こはLoss Functionの![]() だろう.
だろう.
ここまでで展開した全ての議論はこのLoss Functionを最小化する[4]与えられた非負関数の値を最小化することと, その(然るべき意味の)微分の値を最小化することはもちろん違うが, それらが一致するように(activation … Continue readingためのもので, すなわち推論の結果を正解ラベルに近づけるためのものであった.
その学習 (training) を行う上で土台となるネットワークの学習精度は, 順序を伴うLayerに依存する. 先程の計算グラフからも明らかに, どの順で計算するかでoperatorを適用させる対象が変わってしまうからである (parameterやoperatorの対象が行列の場合, 型が変わるので多分計算自体不能となる).
これを解決するのに, Python 2.7で追加された, 公式には項目が追加された順序を記憶する辞書のサブクラス と説明されている collections.OrderedDict クラスを使う. 実装のpseudo-codeとしては次のようである:
layers = OrderdDict()
layers['Affine1'] = Affine(param1, bias1)
layers['Relu1'] = Relu()
layers['Affine2'] = Affine(param2, bias2)
...この章はこれまでと比較して更に実践向けの話が多く, (通常逆だと思うけど) 理論から入った自分でも人が設計したLayerを実装に組み込めそうな気がする. 気が向いたら自分の筆跡を覚えこませてみようかしら.
Footnotes
| ↑1 | 関数 (operator) をvertex (書籍ではnodeと呼んでいる), 代入 (value assignment or calculation) を edge とする有向グラフ. |
|---|---|
| ↑2 | 幾つかのnodeとedgeをまとめて一つのnodeにしたもの. |
| ↑3 | 数値微分と絶対差をepochごとに取って, 誤差逆伝播法の実装の正しさを評価すること. |
| ↑4 | 与えられた非負関数の値を最小化することと, その(然るべき意味の)微分の値を最小化することはもちろん違うが, それらが一致するように(activation functionに単調性を課す等して)調整してるように見える. |

![Rendered by QuickLaTeX.com \[\begin{cases}& \frac{\partial Y_j}{\partial x_i} = w_{ij} \quad (1\leq i\leq m), \\& \frac{\partial Y_j}{\partial w_{kl}} = \delta_{jl} x_k \quad (1\leq k\leq m, 1\leq l\leq n).\end{cases}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-1bbfc9f663cae57ad8d1dcb105bf0ba4_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\partial Y}{\partial (x_1,\ldots, x_m)} = \begin{pmatrix} \frac{\partial Y_1}{\partial x_1}&\ldots&\frac{\partial Y_1}{\partial x_m} \\ &\ddots& \\ \frac{\partial Y_n}{\partial x_1} &\ldots & \frac{\partial Y_n}{\partial x_m} \end{pmatrix} = {}^t W\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-6730ae515def9c0214eb0c0fdeec69ca_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\partial Y}{\partial (w_{11},\ldots, w_{mn})} = \begin{pmatrix} \frac{\partial Y_1}{\partial w_{11}} & \frac{\partial Y_1}{\partial w_{21}} & \ldots & \frac{\partial Y_1}{\partial w_{m1}} \\ &&\ddots & \\ \frac{\partial Y_n}{\partial w_{1n}} & \frac{\partial Y_n}{\partial w_{2n}} & \ldots & \frac{\partial Y_n}{\partial w_{mn}} \end{pmatrix} = \begin{pmatrix} x_1& x_1 & \ldots & x_1 \\ && \ddots & \\ x_m & x_m & \ldots & x_m \end{pmatrix}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-707469652869b1ceb5d4791c23a56b87_l3.png)
![Rendered by QuickLaTeX.com \[\begin{pmatrix} x_1 \\ \vdots \\ x_m \end{pmatrix} = {}^t X\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-b4aaa899814cdf7b8108549a0d99ea7c_l3.png)