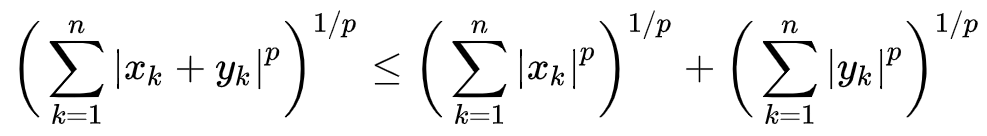Measure theory: convergences and inequalities summary

We summarized classical (yet prominent) results in measure theory for easy reference. Please consult the proofs and comprehensive descriptions on the 2nd edition (2008) of Kiyoshi Ito’s book (ISBN978-4-7853-1304-3).

Relationships between various convergences

For a measure space $(X,\mathcal{B},\mu)$ , let $\{f_n\}$ be a sequence of $\mu$ -measurable complex functions and $f$ a $\mu$ -measurable complex function. Then the followings hold:

No	Notation	Definition	Implications	Extra Conditions
1	converge $\mu$ -a.e.	$\exists E_0\subset X$ with $\mu(E_0)=0$ s.t. $\lim_n f_n = f$ on $X-E_0.$	If $\mu(X)<\infty$ , 1 implies 2. If $f,\,\{f_n\}$ are integrable, 1 implies 4.	–
2	converge asymptotically (converge in a Fréchet space $S(X)$ ).	$\forall \epsilon>0$ , $\displaystyle\lim_{n\to \infty}\mu(X(\|f_n-f\|>\epsilon))=0.$	2 implies 1 for some subsequence $\{f_{n(k)}\}$ .	–
3	uniformly converge $\mu$ -a.e. (converge in a Banach space $M(X)$ ).	$\\|f_n-f\\|_\infty\to 0\,(n\to\infty)$ where $\\|f\\|_\infty={\rm ess.sup}_{x\in X}\|f\|$ = $\inf \{\alpha\geq 0:\|f\|\leq \alpha\ a.e.\}.$	3 implies 1. If $\mu(X)<\infty$ , 3 implies 4.	–
4	converge in mean (converge in $L^p$ )	$\\|f_n-f\\|_p\to 0\ (n\to \infty)$ where $\displaystyle\\|f\\|_p=\{\int \|f(x)\|^p\,d\mu\big\}^{1/p}.$	4 implies 2.	$f,\,\{f_n\}$ are integrable.

Meanings of classical inequalities

No	Name	Claim	Interpretation
1	Cauchy–Schwarz	$\forall f,\,g\in L^2$ , $\|(f,g)\|^2\leq \\|f\\|^2_2\cdot \\|g\\|^2_2.$	Characterize $L^2$ as a Hilbert space (complete norm).
2	Hölder’s	$\forall f\in L^p,\,g\in L^q$ with $p>0,\,\frac{1}{p}+\frac{1}{q}=1$ , $\displaystyle\|\int fg\,dx\|\leq \\|f\\|_p\cdot \\|g\\|_q.$	Product of functions v.s. product of p-norms.
3	Minkowski	$\forall f,\,g\in L^p$ with $p\geq 1$ , $\\|f+g\\|_p\leq \\|g\\|_p+\\|g\\|_p.$	Subadditivity (triangle equality) of norm $\\|\cdot \\|_p$ .