oowriterで横線がしつこくて困った. —が横線に置き換わるのは便利なのだが, なんとBackspaceでもDeleteでも消えない.
——————————————————
今日は可換環というより数論の内容だが, p進数(p-adic number)とその表現について備忘(時々所見)を述べる. 位相については次回に言及したい. p進展開とp進法展開は整数に関しては違いがない. p進展開はp進法展開の整数からp進数体への拡張と見れる.
まず順系と逆系について導入するために, 以下Iを有向集合とする. これは半順序集合であって, ![]() を満たすものである. 群と準同型の族
を満たすものである. 群と準同型の族![]() が存在し, 準同型の族がそれぞれ
が存在し, 準同型の族がそれぞれ
![Rendered by QuickLaTeX.com \[f_{ij}: \begin{cases} A_i\rightarrow A_j\ (direct) \\ A_j\rightarrow A_i\ (inverse) \end{cases} ,\forall i\leq j\in I\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-6d49d8f7c702a5f95f44aeb2d553ff00_l3.png)
と定義されるとき, 以下の性質:
(1) ![]()
(2) 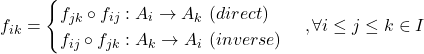
を満たす対, ![]() をI上の順(逆)系という.
をI上の順(逆)系という.
順系では群の族として加群を考えるので,
![Rendered by QuickLaTeX.com \[C=\begin{cases} \bigsqcup_{i\in I} A_i \ (direct) \\ \prod_{i\in I}A_i \ (inverse) \end{cases}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-75cf047861bf4cd8210c41449610435c_l3.png)
をそれぞれに応じて定める. Cは加群の直和, あるいは群の直積群である. このときDを
![Rendered by QuickLaTeX.com \[D=\begin{cases} \big\{ x_i-f_{ij}(x_i) : \forall i\leq j\in I,\ x_i\in A_i\big\}\ (direct) \\ \big\{ x_i-f_{ij}(x_j) : \forall i\leq j\in I,\ x_i\in A_i\big\}\ (inverse) \end{cases}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-c75f7d597a3571ecbf4d3dc5fda1e569_l3.png)
(の右辺)で生成されたCの部分群と見て(あくまでDと書くことにする), 剰余群
![Rendered by QuickLaTeX.com \[C/D=\begin{cases} \lim_{\rightarrow}A_i\ (direct) \\ \lim_{\leftarrow}A_i\ (inverse) \end{cases}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-c3e5b4fb6fa1344f5c334164dfca2fcf_l3.png)
をそれぞれ順(逆)系の順(逆)極限と呼ぶ.
——————————————
以下p進数を考えるのに, 逆系のみ使う.
整数環Zにおける素数pによる局所化![]() をp進整数環(p-adic number ring)と呼ぶ. 積閉集合を逆にした余談(*1)はさておき, p進整数環
をp進整数環(p-adic number ring)と呼ぶ. 積閉集合を逆にした余談(*1)はさておき, p進整数環![]() の任意の元xは, pと互いに素な整数u, vによって
の任意の元xは, pと互いに素な整数u, vによって![]() と表される. 以下の図式,
と表される. 以下の図式,

が可換になり, 特に下の矢印は同型である. 実際![]() として, 準同型
として, 準同型
![]()
の核が![]() になる.
になる.
![]() のとき,
のとき, ![]() と表せる. このとき上の同型χによるu/vの像は単元であり,
と表せる. このとき上の同型χによるu/vの像は単元であり, ![]() となるものがただ一つ存在する.
となるものがただ一つ存在する. ![]() だから,
だから, ![]() と表せる. 同様の手順で
と表せる. 同様の手順で![]() であるような
であるような![]() を一意に定めることができ, これにより
を一意に定めることができ, これにより![]() を得る. これを(もし可能なら)
を得る. これを(もし可能なら)![]() となるまで続けて, 各
となるまで続けて, 各![]() の係数
の係数![]() を右から左に並べたものをp進数と呼ぶ.
を右から左に並べたものをp進数と呼ぶ.
アルゴリズムとしてはユークリッドの互除法をp進数体上でやるということである.
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} 51 &=& 0 + 3\cdot 17 \\ 17 &=& 2 + 3\cdot 5 \\ 5 &=& 2 + 3\cdot 1 \\ 1 &=& 1 \Rightarrow 51 = 1220_3 \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-06b509a3a8504f666206515671952638_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} 8/15 &=& 0 + 3^{-1}\cdot (8/5) \\ 8/5 &=& 1 + 3\cdot (1/5) \\ 1/5 &=& 2 + 3\cdot (-3/5) \\ -3/5 &=& 0 + 3\cdot (-1/5) \\ -1/5 &=& 1 + 3\cdot (-2/5) \\ -2/5 &=& 2 + 3\cdot (-4/5) \\ -4/5 &=& 1 + 3\cdot (-3/5) \\ & \cdots & \\ \Rightarrow 8/15 &=& 3^{-1} + 2 + 3^2 + 2\cdot 3^3+3^4\ldots = ...12102.1_3 \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-306ee9e355335a0461a558cb02d5ce29_l3.png)
右辺の項が発散し, 左辺が8/15というのは感覚と離れていると感じるが, これはp進収束の意味で正しい. この様にして, 任意のp進数体の元はpの有限負巾およびたかだか加算の正巾の和として一意的に表される.
さて加群の族![]() と写像
と写像![]() は逆系を成す.
は逆系を成す.
p=3とおいたときの逆極限![]() において上の例:
において上の例: ![]() となることを見る. 同型
となることを見る. 同型![]() があるので
があるので![]() とおき,
とおき, ![]() と書けば,
と書けば,

のような加群の列が取れる. これが逆極限によるp進整数環![]() のp進数体
のp進数体![]() への完備化である.
への完備化である.
—————————————
整域⊆被約環(reduced)
Counterexample Let e(≠0,1) be idempotent and K be a field. A=Ke⊕K(1−e) is not an integral domain. Prime ideals of A are p=Ke⊕0 and q=0 ⊕ K(1−e). Elements of A−p are of the form k’e+k(1−e) (k≠0). Ap={b(1−e)/(k’e+k(1−e)) | b,k,k’ ∈K,k≠0} is an integral domain. Also Aq is an integral domain.
命題. AをUFD, ![]() を商環.
を商環. ![]() とする. このとき, XとYは同等である.
とする. このとき, XとYは同等である.
証明. 環の準同型![]() の逆像をとることにより, kの素イデアルはAの素イデアルに写る. また
の逆像をとることにより, kの素イデアルはAの素イデアルに写る. また
- (i) kの全てのイデアルは拡大イデアルである
ことにより, kの任意の素イデアルqはAのあるイデアル![]() で
で![]() と書けるので,
と書けるので,
- (ii)
により, ![]() が成立する. これはkの素イデアルの縮約イデアルは素イデアルでかつSと交わらないことを示すので,
が成立する. これはkの素イデアルの縮約イデアルは素イデアルでかつSと交わらないことを示すので, ![]() .
.
逆に![]() を与えたとき, 整域A/pとその商体が得られる.
を与えたとき, 整域A/pとその商体が得られる.
![]() から,
から, ![]() が空かそうでないかに応じ,
が空かそうでないかに応じ, ![]() が0でないか0であるかが決まる. 詳しくは
が0でないか0であるかが決まる. 詳しくは![]() とするとき,
とするとき, ![]() によって全てのA/pの元が零化される.
によって全てのA/pの元が零化される.
![]() より
より![]() であるから
であるから![]() は零でなく, 整域の局所環はまた整域である(自然な環準同型
は零でなく, 整域の局所環はまた整域である(自然な環準同型![]() はAが整域であれば単射である)ことから, 上の同型の右辺より
はAが整域であれば単射である)ことから, 上の同型の右辺より![]() が整域. つまり
が整域. つまり![]() がkの素イデアルとなる. 故に
がkの素イデアルとなる. 故に![]() ■
■
命題3.2: αを環Aのイデアルとし, S=1+αとおく. このとき![]() は
は![]() のヤコブソン根基に含まれる.
のヤコブソン根基に含まれる.
証明: Sが積閉であることはすぐ分かる. ![]() が単元であることを言う. しかし計算ですぐに,
が単元であることを言う. しかし計算ですぐに,
![]()
がでる. これは単元であるから![]() ■
■
命題3.6: ![]() を環. Σを
を環. Σを![]() なるAの全ての積閉集合Sの集合とする.
なるAの全ての積閉集合Sの集合とする.
このときΣは極大元を持つ. また, ![]() が極大であることは, A-SがAの極小な素イデアルであることの必要十分条件である.
が極大であることは, A-SがAの極小な素イデアルであることの必要十分条件である.
証明: Zorn’s LemmaによりΣが帰納的順序集合であることを示せば極大元の存在が分かる. {1}∈ΣだからΣは空でない. Σは包含について順序集合となるから, その任意の全順序部分集合σにおいて![]() がσの上限を与える. →を示すのにT∈Σを極大元とし, p=A-Tとおく.
がσの上限を与える. →を示すのにT∈Σを極大元とし, p=A-Tとおく.
(l1) pはイデアルである
x∈p, つまり![]() とすると, あるTの元tと自然数nが存在して,
とすると, あるTの元tと自然数nが存在して, ![]() となる. 実際そうでないと仮定すると, t=1とおいて
となる. 実際そうでないと仮定すると, t=1とおいて![]() であるから,
であるから, ![]() がTより大きい積閉集合になり, Tの極大性に矛盾する. そこで
がTより大きい積閉集合になり, Tの極大性に矛盾する. そこで![]() で生成される積閉集合
で生成される積閉集合![]() は0を含む.
は0を含む.
故に![]() . 実際ax=sとなるようなa∈A, s∈Tがあれば, 先の議論により
. 実際ax=sとなるようなa∈A, s∈Tがあれば, 先の議論により![]() . これは矛盾である. 以上からx∈pなら(x)⊂p. 和についても, x, y∈pなら
. これは矛盾である. 以上からx∈pなら(x)⊂p. 和についても, x, y∈pなら![]() . そこで
. そこで![]() なら
なら![]() . これは矛盾であるから
. これは矛盾であるから![]()
(l2) pは素イデアルである
Tの元は積について閉じているので, p=A-Tという作り方から明らか.
(l3) pは素イデアルで極小である
![]() となる素イデアルp’が存在するとする. pの作り方から明らかに
となる素イデアルp’が存在するとする. pの作り方から明らかに
![]()
となる積閉集合T’が存在するが, Tの極大性からT=T’, 即ちp=p’である.
逆にpが極小の素イデアルとする. T=A-pは積閉集合になるので, T∈Σ. TがΣで極大とないとすれば, Tを真に含むΣの部分集合族が空でない. それをΣ’⊂Σとする. 包含順序によってΣ’の全順序部分集合に上限が存在するので, Zorn’s Lemmaによって![]() が存在する. これはΣにおいても極大元である(
が存在する. これはΣにおいても極大元である(![]() による). (l1)-(l3)により, A-Sは極小な素イデアルであるが, それはpの極小性に矛盾する.
による). (l1)-(l3)により, A-Sは極小な素イデアルであるが, それはpの極小性に矛盾する.
———————————————–
*1:
積閉集合を上の局所化とは逆にして![]() とすると, 局所化
とすると, 局所化![]() は, Sが飽和している(
は, Sが飽和している(![]() )ので全商環になる. 一方この場合,
)ので全商環になる. 一方この場合, ![]() は必ずしも整数環Zのイデアルにはならない. というのも任意のx∈Iと任意のa∈Zに対し, ax∈Iであるから, (x)⊂Iで, x, yはSの元でないので,
は必ずしも整数環Zのイデアルにはならない. というのも任意のx∈Iと任意のa∈Zに対し, ax∈Iであるから, (x)⊂Iで, x, yはSの元でないので, ![]() は問題ない. しかしIは加法的に閉じてはおらず, 例えばp=5とし, x=2, y=3∈Iをとれば簡単に反例が作れる(x+y∈S). 実際のところZはPIDであり, 従ってUFDであるのでその局所環のイデアルはZのイデアルの拡大である. つまるところこの環Rにおけるイデアルはpと互いに素なq∈Zであって,
は問題ない. しかしIは加法的に閉じてはおらず, 例えばp=5とし, x=2, y=3∈Iをとれば簡単に反例が作れる(x+y∈S). 実際のところZはPIDであり, 従ってUFDであるのでその局所環のイデアルはZのイデアルの拡大である. つまるところこの環Rにおけるイデアルはpと互いに素なq∈Zであって, ![]() の形をしている.
の形をしている.