昨日は素数を複素数に拡張した複素整数環について考えました.
ガウス整数環とは, Cを環と見做した場合の部分環で次のように定義されます.
Z[i]={m+ni∈C|m,n∈Z}
まずはその性質について基本的なところを見ていき, 素数の整域への拡張である素元を計算するところまでを目標にしましょう.
——————————————————
ノルムN:Z[i]→Nを
N(a+bi)=a^2+b^2∈N
と定義して, Z[i]はEuclid整域になる. すなわちノルムNによって,
(Ei) (∀x≠0∈Z[i])(N(z)>N(0))
(Eii) (∀x≠0,y∈Z[i])(∃q,r∈Z[i])(y=qx+r s.t. N(x)<N(r))
を成立させる q, r∈Z[i]を選ぶことができる. (Ei)は自明.
(Eii)は演算が多少煩雑なので, 具体例を出して示す.
まずN(xy)=N(x)N(y)である.
実際x=x+x’i, y=y+y’iとして,
![]()
だからこれは正しい.
今例えば
y=4-3i
x=1-i
とすれば,
y/x=1/2(4-3i)(1+i)=(7+i)/2であって,
a=7/2, b=1/2とおけば,
y=(a+bi)x.
ここで r=xδ (N(δ)<1)なるδ∈Cを適当にとれば,
N(r)=N(x)N(δ)<N(x)が満たされる.
a≡3, b≡1 (mod 2) であるから q=3+i とおいて,
a+bi=q+δ
とすると δ=(a-q_1)+(b-q_2)i = 1/2-i/2となり, N(δ)=1/2<1
を満たす. そこで
y=4-3i
=(a+bi)x =(q+δ)x =qx+r
=(3+i)x-i (q,r∈Z[i]; N(x)>N(r))
なるq,rが取れた.
一般には y/x = a+bi (a,b∈Q) に対して
δ=(a-m)+(b-n)i (s.t. |a-m|, |b-n|≦1/2 ; m,n∈Z)
を満たすように(m,n)を選んで q=m+ni とおけば, 上記例と同様の手順で
y=(a+bi)x=qx+δx (N(x)>N(δx)) となるように定めることができる.
従ってZ[i]はEuclid整域である.
—————————————————————-
Euclid整域は単項イデアル整域で, 単項イデアル整域は素元分解整域である.
つまりZ[i]は素元分解整域であって, 0と単元を除く任意の元が, 単元倍を除いて一意的に素元の積に表示される.
これは有理整数環では, 符合(±)さえ無視すれば, 0と1以外は素数の積に書け, しかもその表示(素数とその指数)が一意的であることに他ならない.
実際単元とは積を演算として逆元をもつ元なので, 有理整数環では単元は{1,-1}のみ(1*1=(-1)*(-1)=1).
e.g.
18=(±2)*(±3^2)
21=(±3)*(±7)
一方ガウス整数環では単元が{±1,±i}の4つ存在するので, 素元分解(⊃素因数分解)の一意性を言うために「±1と±iの倍数を無視して」という但し書きが付く.
このことを使って, 次の命題を示したい.
Proposition. 1)
N(x)が素数であることは, x∈Z[i]が素元であるための十分条件である.
Proof)
Z[i]が素元分解整域であるので,
(∀x∈Z[i] s.t. 0≠x![]() )(x=
)(x=![]() )
)
と表される. ここでaは単元(a∈Z[i]^×), p_λ∈Z[i]は素元である. 従って
N(x)=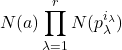
となる. N(a)=1であって, 左辺が素数であれば右辺は1と(ただ一つの)素数の(ただ一回の)積にしか書けず (p_λが素数だから), あるηが存在して
x=p_η
である. 仮定からp_ηは素元であるから題意が示される.
Proposition. 2)
3はZ[i]における素元である.
Proof)
N(3)=9は素数でないから, 命題1は使えない. 一方i≠jに対してp_i=p_jとなるような重複を許せば![]() といずれにせよ素元の積に書け,
といずれにせよ素元の積に書け,
9=N(3)=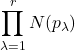
と表示される. 今p_1≠3ならば, N(p_1)N(p_2)=9からN(p_1)=N(p_2)=3でなくてはいけない. しかしm^2+n^2=3なる整数m,nの組は存在しないから p_1=3. すなわち3は素元である.
—————————————————————
次の命題は次回示します:
単項イデアル整域における素元の剰余環は体を成す.
簡便のためにR=Z[i]とおくと, 3が素元であれば剰余環R/R3は体になる. 剰余体R/R3は R∽Z×Zi からR/R3∽Z/Z3×iZ/Z3を導いて位数9をもつ.
続く