先日は図形XとY(位相空間XとYとしても良い)のホモトピー型の一致を確かめる復習をし, 結果曖昧だった部分がかなりクリアになりました.
今週から解析に戻ります.
——————————————-
①まずXとYが同相であれば, bijectionalな連続写像 f:X→Y, g:Y→X がとれるので明らかに ![]() ,
, ![]() であってホモトピー同型.
であってホモトピー同型.
②次にX, Y両方が単体分割可能であれば, 各々の複体K, K’のホモロジー群を計算し, それが不一致なら直ちにホモトピー型が異なることが分かる. これは連続写像 f:X→Y, g:Y→Xに対して定まるホモロジー群準同型 f*:H*(K)→H*(K’), g*:H*(K’)→H*(K)と, 各ホモロジー群の恒等写像にホモトープな(gf)*:H*(K)→H*(K), (fg)*:H*(K’)→H*(K’)を調べると出る. 具体的には, (gf)*と(fg)*が恒等写像である(ホモロジー群準同型としてはホモトープな別の連続写像, この場合恒等写像に一致する)ことと, (gf)*=(g*)(f*), (fg)*=(f*)(g*)からf*とg*はホモロジー群の同型を与え, ホモトピー同型がホモロジー群の同型を与えることからその対偶によって分かる.
ホモロジー群の計算例として, 例えば皿に4つのわっかを付けた図左のような図形のホモロジー群を決定してみよう. 図右のような単体分割を取っておく.
右の図形をX, 十字型の部分を![]() , わっかの部分を
, わっかの部分を![]() , その共通部を
, その共通部を![]() とする.
とする.
![]() の全ての連結成分は単体分割として単体複体を取れるので,
の全ての連結成分は単体分割として単体複体を取れるので, ![]() の連結成分のホモロジー群は非輪状である. 故にmayer-vietorisの短完全列として
の連結成分のホモロジー群は非輪状である. 故にmayer-vietorisの短完全列として
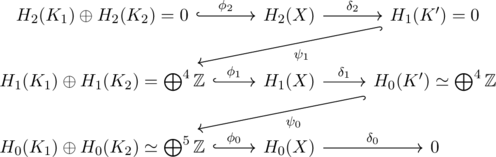
がとれる. ![]() は完全性から同型なので
は完全性から同型なので![]() .
.
![]() は全射で
は全射で![]() .
.
以上からホモロジー群
![]()
が求まった(訂正: 13/12/03).
※図形間の連続写像から定まるホモロジー群準同型を構成する際に, 単体近似を経由する理由は, 単体写像は連続写像だが, 連続写像は一般に単体写像でないからだ. 単体写像が決まれば鎖準同型を構成でき, 鎖準同型からホモロジー群準同型を構成できるので, (i) 任意の複体Kは, 重心細分によってそのホモロジー群は不変, (ii) 単体近似定理により十分細かい細分によって連続写像から単体近似⊂単体写像を構成できる.
③単体分割ができない図形については, そのホモロジー群を求める手法は一般的には知られていない. しかしホモトピー型の一致を確かめるだけであれば, 一方から一方への埋め込みが存在し, 局所的に単体分割可能であったり, n次元球面![]() の貼り合せで実現できるようであれば, 写像度を比較する等によって判断が下せる.
の貼り合せで実現できるようであれば, 写像度を比較する等によって判断が下せる.
【レンズ空間について】
3次元球面を2次元複素空間に埋めこんで
![]()
のように見做す. 互いに素な自然数の組![]() について
について
![]()
と定めれば, ![]() は恒等写像(これは明らかだと思う). 同値関係
は恒等写像(これは明らかだと思う). 同値関係![]() によって定まる商空間
によって定まる商空間![]() をレンズ空間という.
をレンズ空間という.
Proposition: ![]() は固定点を持たない. またレンズ空間における同値類は丁度p個の元から成る.
は固定点を持たない. またレンズ空間における同値類は丁度p個の元から成る.
Proof: ![]() と書くことにすれば,
と書くことにすれば, ![]() であって
であって![]() が成り立つことが確かめられる. 第二要素についてもqがpで割り切れないという仮定から,
が成り立つことが確かめられる. 第二要素についてもqがpで割り切れないという仮定から, ![]() から同様のことが成り立つ.
から同様のことが成り立つ.
一方, ![]() は
は![]() の相異なるp個の根である(代数学の基本定理). 逆に
の相異なるp個の根である(代数学の基本定理). 逆に![]() の根となるような
の根となるような![]() の元を同一視したものが
の元を同一視したものが![]() であるから, それらp個の根が同値類の元を与える■
であるから, それらp個の根が同値類の元を与える■
重要な4種の群作用をまとめておく.
<群→集合>
群G(∋g,h,e), 集合X(∋x)に対し,
G×X→X ((g,x)→gx)
(i) (gh)x=g(hx) (結合)
(ii) ex=x (単位)
※右作用の場合は(gh)x=h(gx)となる. 作用の順番がg→hなので, x(gh)=(xg)hと書いた方が直感的.
φ: G→S(X)によって, (g,x)→φ(g)xと定義しても同じ.
<集合→群>
集合(作用域)Λ(∋λ), 群G(∋x,y)に対し,
Λ×G→G ((λ,x)→λx)
(i) λ(xy)=(λx)(λy) (結合: Λ=環と考えればむしろ分配)
Λ準同型: f(λx)=λf(x): G→G'(Λ群→Λ群)
Λ部分群: 部分群H⊂Gに対し, λh∈H.
φ: Λ→EndGによって, (λ,x)→φ(λ)xと定義しても同じ.
※右作用の場合は(gh)x=h(gx)となる. 作用の順番がg→hなので, x(gh)=(xg)hと書いた方が直感的.
φ: G→S(X)によって, (g,x)→φ(g)xと定義しても同じ.
<群→群>
群G⊃H,K(部分群)に対し,
H×G→G ((h,x)→hx) := 左移動
(H×K)×G→G (((h,k),x)→hxk^(-1)) := 左作用
G×G→G ((g,x)→i_g(x), i_g∈IntG) := 内部自己同型
<環→加群>
環R(∋a,b), 加法群M(∋x,y)に対し,
R×M→M ((a,x)→ax)
(i) a(bx)=ab(x) (結合)
(ii) ex=x (単位)
(iii) (a+b)x=ax+by (分配1)
(iv) a(x+y) =ax+ay (分配2)
———————————————–
Proposition: 素数pに対し, p元体Fpは代数閉体でない.
Proof: 定数でないFp上の多項式f(T)∈Fp[T] (deg(f(T))≧1)の根がFpに含まれないようなf(T)をうまく取って反例とする.
f(α)≠0 (∀α∈Fp)を満たせば良いので, f(T)=T^p-T+1とすればα^p=α(∀α∈Fp)でf(α)=1≠0で十分■
Proposition: ![]() は代数閉体.
は代数閉体.
Proof: 結論としては, 任意に取った多項式![]() の根がK上の代数的数で生成されることを言う. まず
の根がK上の代数的数で生成されることを言う. まず![]() がΩの部分体となるのは, K上の任意の代数的数α,β,…∈
がΩの部分体となるのは, K上の任意の代数的数α,β,…∈![]() が生成する集合がKの代数拡大K(α, β, …)/Kであること(定義による)と体の定義から, α+β, αβ, α/β, -α∈
が生成する集合がKの代数拡大K(α, β, …)/Kであること(定義による)と体の定義から, α+β, αβ, α/β, -α∈![]() , つまりそれらは代数的なので部分体として閉じていることから分かる.
, つまりそれらは代数的なので部分体として閉じていることから分かる.
次にα∈Ωについてf(α)=0 (![]() )を満たせば, αは
)を満たせば, αは![]() 上代数的(このようなαはΩが代数閉体であるから必ず存在する), 従って
上代数的(このようなαはΩが代数閉体であるから必ず存在する), 従って![]() 上も代数的 ∴α∈
上も代数的 ∴α∈![]() ■
■
Q(√2,√3)上の代数的数α=√2-√3をとる(最小多項式φ_α(T)=T-α)と, αはQ(√2), Q(√3), Q上代数的である(多項式T^4-10T^2+1が, どの中間体においても最小多項式を因数に持つ).
Proposition: 代数拡大M/K(L⊃M⊃K)で, M上代数的なα∈LはK上も代数的である.
Proof: 一般的な証明は直感的でないので, 上の具体例を使って示す. 代数拡大M/Kがあるとき, M上の代数的数α∈Lの最小多項式φ(T)を考えると, φ(T)の各係数{a_i}はMの元で(上記例では√2,√3がQ(√2,√3)の元であるということ), Mの元はK上代数的であるからたかだか有限回の加減乗除によって{a_i}をKの元に移すことができる(上記例ではQ(√2)∋√2^2=2∈Q, Q(√3)∋√3^2=3∈Qのようにできる). a_iをKの元に移す(勿論K上の)最小次数のモニック多項式をc_i(T)∈K[T]とし,
![]()
とおけば,
![]()
とできる.
![]() はK[T]の元なので, これをn回繰り返せばφ(T)をK[T]の元に移せる■
はK[T]の元なので, これをn回繰り返せばφ(T)をK[T]の元に移せる■

