日記: 1と3の日 – 13/3/13

いやはや、お久方です。

今日いとこを通じて知り合ったサッカー仲間の友人にばったり再会した。
彼は急いでいたようで暫くして別れたが、話し振りから私生活がすごいことになっているようだ。近々時間をとって話してみたいと思った。

そして区役所の方に向かったものの、人が多いので仕方なく長机に座った。

最近は特に保型形式を理解したくて(それを理解すればどういうことに役に立つのか具体例を挙げられるほどにも理解していない)、多様体と表現論(テンソル、微分形式等)を復習及び追加学習しているのだけど、計算が繊細でちょっとの間違いを気づかずそのままにしておくと、後で大きなロスになるので全く気が抜けない。

高校生にもなじみの「合成関数の微分」ひとつとってもそうで, 未だに多変数関数を合成したときは冷やっとなる。
例えば, n個の合成可能関数が $\mathbb{R}^s$ 上のs次元 $C^r$ 級可微分多様体Mにおける或る座標近傍V上で定義されているとき, すなわち:

$f_l(x_{l1},x_{l2},\ldots) \qquad (x_{\eta,j}=f_{\eta-1,j}; 1\leq l \leq n; j\geq 1; 2\leq \eta\leq )$

に対し,

$\phi_n=f_n\circ \cdots \circ f_1:V\rightarrow M$

がV上の $C^1$ 級関数として意味を持ち, その第 $i_1$ 局所座標を変移させたときに影響される $k(\eta)$ 個の $x_{\eta,j}$ を $x_{\eta,i_{\eta,1}},\ldots,x_{\eta,i_{\eta,k(\eta)}} \quad (1\leq \eta \leq n)$ とすると, $i_1$ による偏微分 $\displaystyle{\frac{\partial \phi_n}{\partial x_{1,i_1}}}$ が次の形になる.

$\displaystyle{\frac{\partial \phi_n}{\partial x_{1,i_1}} = \sum_{\binom{i_{\eta,1}\leq j_\eta \leq i_{\eta,k(\eta)}}{2\leq \eta \leq n}}(\frac{\partial f_n}{\partial x_{n,j(n)}}\circ f_{n-1})(\frac{\partial f_{n-1,j(n)}}{\partial x_{n-1,j(n-1)}}\circ f_{n-2})\cdots (\frac{\partial f_{2,j(3)}}{\partial x_{2,j(2)}}\circ f_1) \frac{\partial f_{1,j(2)}}{\partial x_{1,i_1}} }$

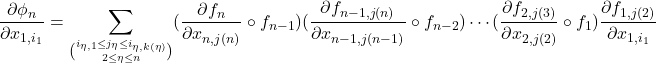
この変数の多重構造がこちらをいっそう疲れさせる！

気分転換にピアノは相変わらず弾くんだけど、

気分転換は気分転換。

二足のわらじはやはり履けないな(笑)