引越し等で忙しいです.
下は本日学習の途中でやっつけていった補題です.
——————————————
これは新課程高校数学の内容で, 約数の和と個数を手際よく計算するもの.
分かりやすい説明になるよう心がけた.
時間があればMöbius関数も扱いたかったが, またの機会にする.
自然数nが素因数の積としての表示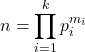 を持つとき, その約数d_j (1≦j≦d)について次のことが成り立つ.
を持つとき, その約数d_j (1≦j≦d)について次のことが成り立つ.
(i) 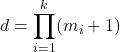
(ii) 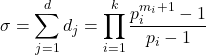
証明)
(1) 各p_iを選ぶ方法がm_i+1個(選ばない場合を一つと数え, 0個, 1個, …, m_i+1個)で, しかもp_iの選び方は他のp_j (i≠j)の選び方に関係しないので, 積の法則が適用されて公式を得る.
(2) 各p_iのどれを選ぶかは約数の作り方に関係しない(すなわち約数の作り方は各素因数の個数のみに関係する. 例えば12=2^2*3の場合, 2を0, 1, 2個選ぶ3パターンと3を0, 1個選ぶ2パターンの組み合わせでのみ決まるが, 2が2回掛かってるからといって1個選ぶ場合, 2_0, 2_1等と区別したりしない). そこでj番目の素因数p_jをi_j個含む約数について(0≦i_j≦m_j, 1≦j≦k),
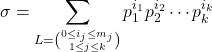
である. ここで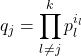 , 即ち上の式の右辺において第j番目の素因数を除いたものをq_jとすれば,
, 即ち上の式の右辺において第j番目の素因数を除いたものをq_jとすれば,
![]()
Lからjに関する条件のみを除いたものをL\L_jと表わせば,
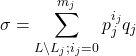
は明らかにp_jに関する等比数列の和に等しい(i_jが0からm_jまで動くときq_jは動かないので, 初項をp_j^0*q_j=q_j, 公比をp_jと考えることができる).
このことから結局,
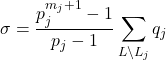
を得るので, この操作をk回繰り返せばLは空になり, 公式が得られる■
———————————
続いて有名な積分公式を扱う.
n次元表面積, 体積を求める過程が一般化される応用を持つ, Dirichletの積分と呼ばれているものである.
0を除いたn次元開球を D={x∈R^n|x_i>0, ∑[i=1,n]x_i<1} と定義する.
連続関数 f:(0,1)→R に対し, t^(p-1)f(t) が開区間(0,1)上広義可積分とする (p_i>0, p_0=∑[i=1,n]p_i).
このとき, 次で定義されるDirichletの積分 I=I(p_1,…,p_n ; f)を求める.
I=![]()
まず変数変換
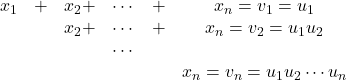
を考える.
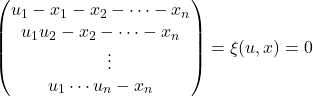
として, uに関するヤコビアンが0でない, すなわち
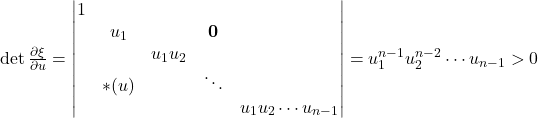
となることからuについて一意に解ける. 同様のことがxについても言え, 次の関係式を得る.
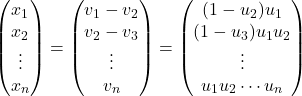
上の u→x 変換をg (x=g(u))とすると, gは E=(0,1)×…×(0,1)→D なる全単射であるから, ![]() .
.
![]()
から,
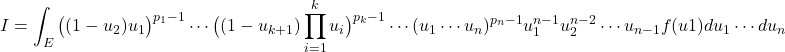
ここでu_iの(単項としての)次数は
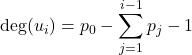
となるので, u_iを含む項t(u_i)は結局
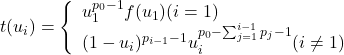
となる. i≠1のときの開区間(0,1)における広義積分はベータ関数によって
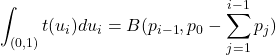
と表示されるので, 2≦i≦nまでを掛け合わせれば,
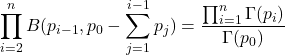
を得る(u, x, pの定義から範囲内でベータ関数が広義一様収束することは明らか).
以上から次を得る.
![]()
![]() .
.
———————————————–
行列の要素表記を変えたときの演算法則.
断らない限りA, Bをn次正方行列(A,B∈Mn(K))とする.
同様に小文字のアルファベットでjを添字として持つものをn次元数縦ベクトルとし, プライム付き(v’)は横ベクトル(転置ではない)とする. 転置はt(*)で表し, 2次元で記述したものについてはそれがn次元に拡張されても同様のことが成り立つので, 簡単のために2次元で記述されていることとする.
A=(a_1,…,a_n)=t(a_1′,…,a_n’)=(a_ij),
B=(b_1,…,b_n)=t(b_1′,…,b_n’)=(b_ij)
に対し,
AB=(Ab_1,…,Ab_n)=(∑[k=1,n]a_ik b_kj)
AB=(∑[i=1,n]a_i b_i1,…,∑[i=1,n]a_i b_i1)
AB=(∑[j=1,n]a_1j b_j’,…,∑[j=1,n]a_1j b_j’) (横に並べてるが, これはABの各行に対応している)
AB_j=∑[i=1,n] (a_i’, b_j)e_i=∑[j=1,n] a_j b_ij
——————————————–
ここから解析の諸命題をおおざっぱに見ていく.
命題: ![]() 上の正則関数f(z)の収束半径は(複素)微分によって不変.
上の正則関数f(z)の収束半径は(複素)微分によって不変.
証明: 帰納法によるものもあるが, Cauchy-Hadamardの定理を使う.
仮定によりfは![]() 上Taylor級数表示を持ち, 平行移動
上Taylor級数表示を持ち, 平行移動![]() による収束半径は変わらないから,
による収束半径は変わらないから,
![]()
として一般性を失わない.
fは収束し, その収束半径lは
![]()
となり, 正則であるから一階の微分も収束半径l’>0をもち,
![]()
を満たす.
従って任意のε>0があって十分大きなnについて![]() を示せばよい.
を示せばよい.
![]() であるから(収束するから),
であるから(収束するから), ![]() の上限に
の上限に![]() の取りかたは関係しない(言い換えれば, 数列a_nがnの関数として極大となるような部分列n(p)によるa_nの値, つまりa_n(p)のことを言うが, そのn(p)の選び方は
の取りかたは関係しない(言い換えれば, 数列a_nがnの関数として極大となるような部分列n(p)によるa_nの値, つまりa_n(p)のことを言うが, そのn(p)の選び方は![]() に拠らないとも言える).
に拠らないとも言える).
つまり
![]()
となるので, 上式は
![]()
と等価. これはすぐに示される(fが正則だから![]() が有界である).
が有界である).
実際εの大きさに応じてn=[1/ε], [ε]とおけば, ![]() 等とできる■
等とできる■
—————————————————
次に単調増加連続関数列の一様性をかなり緩い条件で保証するDiniの定理を考えたい. 集合(一般には位相の入った)「コンパクト性」の扱いやすさがよく分かる好例.
Ulisse Dini (1845–1918)
位相幾何学において史上最古の位相不変量として有名な, 各次元における「穴の数」を表現する「ベッチ数」の発見者であるEnrico Bettiの弟子だそう. 解析・幾何が専門のイタリアの数学者らしい.
[Dini’s Theorem]
コンパクト集合K上の連続関数列(f_n)_{n∈N}が次の(i), (ii)を満たすと仮定する.
(i) 任意のx∈Kに対し(f_n(x))_{n∈N}は単調増加(または減少)数列.
(ii) (f_n)_{n∈N}はK上の連続関数fにK上各点収束する.
このとき, (f_n)_{n∈N}はfにK上一様収束する.
証明のあらすじは,
①任意のxをKから選んで, xの近傍上f_nを各点収束させることができる(仮定)
②各点収束するような添字nがx, つまり近傍の取り方に依存するが, その近傍U(x,δ(x))を含むような開集合Vを, f_nの各点収束性が崩れないだけ十分大きくとる.
③定義から, そのようにして取ったV上f_nはfに各点収束する. もしそのようなVがKを覆うならば, nはもはやxに依存していないのでf_nはK上fに一様収束する(||f-f_n||<ε). しかしここではVがKを覆い切らないとする.
④Kのコンパクト性から, Vを含むKの開被覆のうち, 有限個の開集合から成るものがとれる.
⑤開被覆(V_i) (1≦i≦m)で, あるjで②を満たすVに対し U(x,δ(x))⊂V_j⊂Vを満たすようなものが存在する.
⑥(x_1,…,x_m)∈V_1×…×V_m に対しMax(n(x_1),…,n(x_m))=nとおけば, nはn(x_j)≦nを満たすから, f_nが収束するようなxに依存しない添字となる.
⑦単調増加性から f_n(x_i)≦f_n≦f で, ||f-f_n||<||f-f_n(x_i)||<ε■
有限被覆性は興味深いので, この議論を集合論的考察に置き換えてもう少し詳しく見てみよう.
命題: Sの部分集合Uが性質(条件)C=C(U)を持つとき, Cを持つSの極大部分集合V⊃Uが存在するために, Cが有限的な性質であることが十分である(Turkey).
※有限的な性質Cとは, ある集合Χの部分集合に関する性質Cがあって, Χの部分集合Yがその性質Cを持つことと, Yの全ての有限部分集合が性質Cを持つことが同等であるようなものを言う. Diniの定理の例ではΧとはK, C(U)とはn>n(x) (∃x∈U)⇒f_nがfに各点収束することで, n(x)は「f_nがxの近傍で各点収束するような十分大きなn」と定義したから, その近傍に含まれる有限部分集合は全て性質C(U)を持つことになり, C(U)は有限的である.
証明: Cを満たすようなΧの部分集合全体をΨとすれば, Ψは包含順序において帰納的順序集合である. 実際NをΨの任意の全順序部分集合とすれば, ∪N={L|L∈N}=N*とおいて N*∈Ψで, これはΨにおけるNの上限を与える. N*∈Ψであることは次のようにして確かめられる.
N’={x_1, …, x_r}をN*の任意の有限部分集合とすれば, x_i∈N_iとなるNの元N_i (i=1,…,r)がある(Nは全順序部分集合系であるから, その元は集合). それらは包含関係について全順序集合をなすので, N_1,…,N_rの内最大の集合がある. それを仮にN_rとおけばN’⊂N_rとなり, N_rはCを満たすのでCの有限性によってN’もCを満たす. したがってまたN*⊃N’もCを満たす. よってN*∈Ψとなり, (Ψ,⊂)は帰納的順序集合であることが分かる. 即ちZornの補題からΨは極大元を持つ■
