最近は, ホモロジー代数でも構成の正しさを調べる手段が重要なことが多く, 特に代数的構成は詳しく知っておきたい.
命題: 直和の構成とテンソル積の構成は可換である
証明: 同型![]() を示せばOK.
を示せばOK.
Balanced map ![]() を
を![]() と規定すれば,
と規定すれば, ![]() が自然なバランス写像
が自然なバランス写像![]() に対し引き起こす写像
に対し引き起こす写像![]() で, 次の図式を可換にするものが一意的に定まる.
で, 次の図式を可換にするものが一意的に定まる.
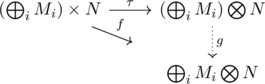
実際任意の![]() に対し,
に対し, ![]() は一意的に定まる.
は一意的に定まる.
更に, Balanced map ![]() が引き起こす準同型
が引き起こす準同型![]() についても同様のことが成り立つ.
についても同様のことが成り立つ. ![]() として一意性と普遍性を保ったまま拡張することができるので, 可換図式
として一意性と普遍性を保ったまま拡張することができるので, 可換図式
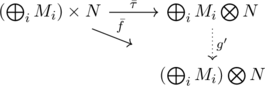
を得る(![]() は直積と直和の可換性から).
は直積と直和の可換性から).
このときBalanced mapの与え方は任意であったので,
![]()
とおけて, ![]() と一意性から,
と一意性から,
![]()
が同型を与える■
命題: 有限生成射影的左R加群Mと, 任意の左R加群Nに対し,
![]()
が成立する.
証明: ![]() が同型対応であることを見たい.
が同型対応であることを見たい.
まず左R加群Mの双対加群![]() は, 右R作用
は, 右R作用![]() により, 右R加群の構造をもつ.
により, 右R加群の構造をもつ.
Mが有限射影的であるから, 自由加群Fの直和因子であって![]() . さらにAbel群の双対性によって,
. さらにAbel群の双対性によって, ![]() が成立している.
が成立している.
∵![]() が全単射であることから分かる.
が全単射であることから分かる.
また一般に, 右R自由加群と左R加群とのテンソル積は, 自由加群の階数rに対し, 左R加群のr冪に同型(![]() )で, 自由加群はその双対と同型である(基底の準同型を考える必要がある).
)で, 自由加群はその双対と同型である(基底の準同型を考える必要がある).
これらのことを合わせると, 次の等式が成り立つ.
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} \hat{F}\otimes_R N & \simeq$ & N^n \quad (n={\rm rank}\hat{F}) \\ &\simeq & Hom_R(F,N) \quad ((x_1,\ldots,x_n)\mapsto (pr_{x_1},\ldots,pr_{x_n})) \\ &\simeq & Hom_R(M,N) \oplus Hom_R(M',N) \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-daa30237f6d9fdbd14f369f704ea47c1_l3.png)
さらに次の図式も可換になる.
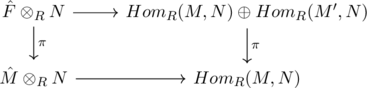
以上から同型![]() が得られた■
が得られた■