論証を既に終え、正当性が認められた数学的形式的手続きを「計算」と呼ぶことにしよう。
その計算手続きが極めて煩雑になり、記法・表現が重複していたり多様であったりすると、計算上の間違いは回避が難しいだろう。
それを回避するためにどのような工夫がなされ、そしてなされていくべきだろう?
多変数(ベクトル)解析における簡約記法はその工夫の好例であると思える。
行列論はベクトル空間における基底変換を効率的に行わせるという一面がある。ベクトル空間Vを固定して群のある元に対しVの自己同型群の元を対応させる群の表現も、既約表現という正規化された一意的な表示を与える。束論におけるモジュラー束の射影幾何に対する応用は、joinとmeetで幾何的な交叉条件を形式的代数演算で書けるようにする。
さて、先月から請け負っている仕事の関係でデータベースを触ることが多くて、寄り道と分かっていつつも変なことを考えていた。
与えられた自然数でユニークなIDが作れないかということを。
もちろんユニークなIDを具体的に作りたかったのもあるが、それよりも個人的な関心として、価値のあるユニークIDの作り方があるとすればどこにあるか、その辺を推測してみたいと考えた。その内容は大体次のようなものだ。
桁に対応した次元の整数係数ベクトル空間に或る「標準形」を導入して、「標準化」されるまでの線形変換の列から自然数への対応を作ってはどうか。ある標準形が与えられた場合、それに標準化するまでの行程は一つでなくても、標準形は並び替え(と符号)を除いて一意的に定まる。自然数への1対1対応を作ろうと思ったら、標準化の仕方に(右変換のみ等の)制限を加える必要はあるだろうと思われる。
4桁の数字(0は0000と書くことにする)を例にとって上に書いた手法の一例を検証してみよう。
例えば4桁の各数を左から右、上から下へ行列に当てはめたものと元の4桁の数を同一視した場合、
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} 23&=&0023\sim \begin{pmatrix}0&0\\2&3\end{pmatrix},\\ 203&=&0203\sim \begin{pmatrix}0&2\\0&3\end{pmatrix} \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-78047c4fb4f52a60beb8a4e746442ef8_l3.png)
と書ける. この右辺の行列から自然数への対応は一意的でないといけない.
標準形を簡単にJordan標準形の自然数倍(整数の中で考えたいため)と決め、ある行列がその標準形に移るための(右)変換をその行列の標準変換と呼ぶことにする. 上の形では23と203は同じ固有値0, 3を持つが, 異なる標準変換
![Rendered by QuickLaTeX.com \[\begin{array}{l} \begin{pmatrix}3&0\\-2&1\end{pmatrix},\ \cdots (i) \\ \begin{pmatrix}1&2\\0&3\end{pmatrix}\ \cdots (ii) \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-538164e5c21c559e4c77ef18e3c6c77b_l3.png)
をそれぞれ持つことが分かる. しかしこれは固有ベクトルの並べ替えに依存するし、しかも符号という問題がある. そこで逆に23に対応した標準変換(i)の各要素を正数に置き換えたものを標準変換として持つような数を求めてみる. そのような数を![]() と書くと、(ここばかりは逆変換を使うため有理係数を許して)
と書くと、(ここばかりは逆変換を使うため有理係数を許して)
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} && 1/3\begin{pmatrix}1&0\\-2&3\end{pmatrix} \begin{pmatrix}a&b\\c&d\end{pmatrix} \begin{pmatrix}3&0\\2&1\end{pmatrix} \\ &=& 1/3\begin{pmatrix}3a+2b&b\\-6a-4b+9c+6d&-2b+3d\end{pmatrix} \\ &=& \begin{pmatrix}a&0\\0&d\end{pmatrix} \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-89699608a5d3e3ee31bb62a9280be685_l3.png)
を満たさねばならない.
最後の等式はb=0, -2a+3c+2d=0から出る. 標準形としてはb=1も有り得たが, 整数係数行列なのでその場合![]() が成り立たなくなる. ここから計算で
が成り立たなくなる. ここから計算で
![]()
の形であることが分かる. この自由度は2で, 与えられた4桁の数に付随する行列の標準変換の空間による商空間において![]() 等の数が全て同一視されることになる. この結果は上の意味での標準変換に4桁の自然数を対応させても一意的にならないが, 2桁の自然数なら一対一になるということである.
等の数が全て同一視されることになる. この結果は上の意味での標準変換に4桁の自然数を対応させても一意的にならないが, 2桁の自然数なら一対一になるということである.
逆に辿って2桁の数字から始めれば, これは2桁数の空間→4桁数の空間への包含で, 応用があるかもしれないが, もう少し一般的な考察をしたい.
k桁の数の各桁の数の和が作る自然数は1≦n≦9kを動き、最高位桁の数を除いて置換について不変である。つまりk桁の自然数の全体を![]() 、その各桁の和が作る自然数全体を
、その各桁の和が作る自然数全体を![]() と書けば、k次置換群
と書けば、k次置換群![]() の
の![]() への桁の置換に関する作用を下(k-1)桁に制限したものは、写像として
への桁の置換に関する作用を下(k-1)桁に制限したものは、写像として![]() と書け、これは
と書け、これは![]() の上で定値写像である。
の上で定値写像である。
![]() を各桁の積が作る自然数全体としても同様であるから、興味があるのは
を各桁の積が作る自然数全体としても同様であるから、興味があるのは![]() が
が![]() 不変であるようなものである(ここで
不変であるようなものである(ここで![]() 不変とは、
不変とは、![]() が
が![]() を満たすことを言う。
を満たすことを言う。![]() は下(k-1)桁に制限した置換を表す)。そのようなものを
は下(k-1)桁に制限した置換を表す)。そのようなものを![]() と書くと、
と書くと、![]() で、
で、![]() の大きさは、k桁の数から新しい数を作る方法の一つの「単純性」を測る指標となっていると思える。特に積の方で定義した
の大きさは、k桁の数から新しい数を作る方法の一つの「単純性」を測る指標となっていると思える。特に積の方で定義した![]() は、
は、![]() の元として殊更に単純である。というのも0を桁に一つでも含むような
の元として殊更に単純である。というのも0を桁に一つでも含むような![]() の
の![]() 個の数は、
個の数は、![]() 上0に移る。
上0に移る。
![]() をもう少し調べるのに、
をもう少し調べるのに、![]() を自然数の有限部分集合族、
を自然数の有限部分集合族、![]() を桁の数の和で生成される自然数全体として、
を桁の数の和で生成される自然数全体として、![]() で
で![]() を定める。
を定める。![]() は空ではないから
は空ではないから![]() は単射である。ここでの興味は、
は単射である。ここでの興味は、![]() のある意味での連続性である。逆に言えば、
のある意味での連続性である。逆に言えば、![]() が連続になるような最大の位相
が連続になるような最大の位相![]() 、すなわち
、すなわち![]() を連続にする最も粒度の細かい位相において、上の意味での新しい数の作り方の単純性が、それを保ったまま別の作り方へと移る度合いを示すものだ。
を連続にする最も粒度の細かい位相において、上の意味での新しい数の作り方の単純性が、それを保ったまま別の作り方へと移る度合いを示すものだ。
このような性質を持った連続写像と位相空間の対![]() を一つ決め、一意的で応用上意味のある対応が、上の意味で最も複雑な数の作り方に属すると考える。このとき、有限個の単純な数の作り方
を一つ決め、一意的で応用上意味のある対応が、上の意味で最も複雑な数の作り方に属すると考える。このとき、有限個の単純な数の作り方![]() から
から![]() 上最も離れたところにある数の作り方として特徴づけた
上最も離れたところにある数の作り方として特徴づけた![]() の部分集合の中にその対応が含まれるはずである。そこで「単純」な作り方でできた
の部分集合の中にその対応が含まれるはずである。そこで「単純」な作り方でできた![]() を
を![]() 内で動かしたり拡張することができれば、
内で動かしたり拡張することができれば、![]() 内で
内で![]() に「似た」集合系をとることができ、その極限で
に「似た」集合系をとることができ、その極限で![]() を完備化する。その双対から複雑な作り方に分類される対応の普遍的性質が判明しそうに思う、と興味深い内容が山積する.
を完備化する。その双対から複雑な作り方に分類される対応の普遍的性質が判明しそうに思う、と興味深い内容が山積する.
この(数学的になかなか)際どい方針に従ってもう少し調べてみたくなるが、その結果までをブログには書けないかもしれない. まずはその道具を書き下すところから始める. 被覆とか位相群あたりのことが必要になるだろうから.
———————————–
命題: ![]() のホモトピーを
のホモトピーを![]() とする.
とする. ![]() をf(a)からg(a)に至る道として,
をf(a)からg(a)に至る道として,
![]()
で定める. このとき, ![]() が成り立つ.
が成り立つ.
証明の前に, 道wが引き起こす基本群の間の準同型![]() は,
は,
![]() により同型になることに注意する. 次の図式を考えてみよう.
により同型になることに注意する. 次の図式を考えてみよう.
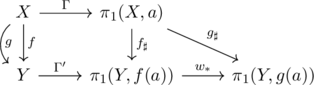
任意の![]() は,
は, ![]() によって, それぞれ次のようにうつる.
によって, それぞれ次のようにうつる.
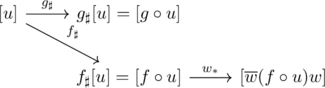
そこで, ホモトピー![]() が構成できれば証明は完了する.
が構成できれば証明は完了する.
上の形から, 欲しいものは
![]()
を満たすホモトピーであるが, 上の要素に関しては与えられたホモトピー![]() が既にそのようなものを与える.
が既にそのようなものを与える.
wについては![]() を作れば良いので,
を作れば良いので, ![]() とおくと, 条件を満たすことが分かる.
とおくと, 条件を満たすことが分かる.
これでホモトピー![]() が構成できたので, 上の等式が示された■
が構成できたので, 上の等式が示された■
命題: ![]() がホモトピー同値なら,
がホモトピー同値なら, ![]() は同型.
は同型.
![]() をホモトピー逆写像として,
をホモトピー逆写像として, ![]() が成り立つ.
が成り立つ.
前の命題を![]() に適用させて,
に適用させて,
![]()
を満たすように道![]() が存在する.
が存在する.
ホモトピー写像として(i)は普遍的で, ![]() を満たす.
を満たす.
これはホモトープな道の対が, 連続写像によって写る像空間においてもまたホモトープな道の対となり, ホモトープである性質は不変であることによる. (ii)も同様で,
(i), (ii)から,
![]()
上は![]() の単射であることを, 下は全射であることを示すので, これは同型である■
の単射であることを, 下は全射であることを示すので, これは同型である■
位相空間Xが単連結であることは, 任意の点における基本群が自明であることで, 可縮な空間は一点集合とホモトピー同値で一点集合は明らかに自明な基本群を持つので単連結となる. 複素解析的には![]() なサイクルΩを領域内で任意に取れる時を言うのであり, これが同値であるのは, 積分値が同じになるようなサイクルの同値類と, 基点を決めたとき, その基点における閉道をホモトピーの関係で割った時の同値類とが本質的に同じものであることが言える.
なサイクルΩを領域内で任意に取れる時を言うのであり, これが同値であるのは, 積分値が同じになるようなサイクルの同値類と, 基点を決めたとき, その基点における閉道をホモトピーの関係で割った時の同値類とが本質的に同じものであることが言える.
被覆射の合成がまた被覆射であるか?という確認を行った. 以下がそれである.
命題; 二つの被覆射![]() の合成
の合成![]() はまた被覆射であるか?
はまた被覆射であるか?
今p, p’は全射であることを仮定する. そうするとq(Y’)=p(p'(Y’))=Xからqも全射. Xの離散位相における開集合U⊂Xに対し, ![]() であるから連続性も言える.
であるから連続性も言える.
従って確認すべきことは, x∈Xの近傍Uの上での自明化![]() が,
が, ![]() を満たすように存在することである.
を満たすように存在することである.
![]() 上のpに関する自明化をh,
上のpに関する自明化をh, ![]() 上のp’に関する自明化をiとおく.
上のp’に関する自明化をiとおく. ![]() は付随しているものとする.
は付随しているものとする.
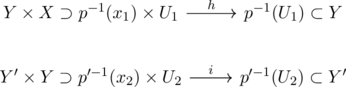
であるから, ![]() がどう写るかを見てみると,
がどう写るかを見てみると,
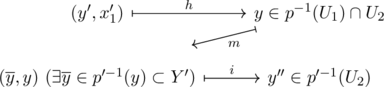
のようになると考えられる.
※mは![]() の元yに対し, 被覆射p’の逆像
の元yに対し, 被覆射p’の逆像![]() の元
の元![]() とyのタプルを写像しているが, もちろんこれは一般的には一意的ではない.
とyのタプルを写像しているが, もちろんこれは一般的には一意的ではない.
しかし, 一意的である条件を付け足すことにして, これでともかく![]() が定義された.
が定義された.
最後にこれで![]() を写像してみると,
を写像してみると,
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} (q\circ k)(y',x_1') &=& p\circ(p'\circ i)\circ m\circ h (y',x_1') \\ &=& p\circ(p'\circ i)(\overline{y},y) \\ &=& p(y)\in p(p^{-1}(U_1)\cap U_2) \subset pp^{-1}(U_1)\cap p(U_2)=U_1\cap p(U_2) \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-bd760020147fb0683d16164f3a0843d2_l3.png)
![]() のときに限り, qは被覆射になる.
のときに限り, qは被覆射になる.
できればシリーズものにしたいが・・ガロア被覆射の構成も少し書きたいと思う.