東京への旅を終えて

気になった問題等.

精密な評価をサボってはまった.
解釈に悩むし.

$\theta\in (0,1),\ z=(x,y)$ とおいて,

$\begin{array}{lcl} \displaystyle{ \int\int_{B_p} du_0} &=& \displaystyle{ \int_0^p r^2dr\int_0^{2\pi} \cos{t}+\sin{t} dt} \\ &=&\displaystyle{\int_0^{2\pi} \cos{t}+\sin{t} dt \int_0^p r^2dr} \\ &=&\displaystyle{o(p^3)\int_0^{2\pi} \cos{t}+\sin{t} dt}\ (p\rightarrow 0) \\ \displaystyle{ \int\int_{B_p} d^2u_0} &=& \displaystyle{ o(p^4)\int_0^{2\pi} \cos{2t}+\sin{2t} dt}\ (p\rightarrow 0) \\ \displaystyle{ \int\int_{B_p} d^3u_{\theta z}} &=& \displaystyle{ o(p^5)\int_0^{2\pi} \cos{3t}+3\cos{t}-\sin{3t}+3\sin{t} dt}\ (p\rightarrow 0) \end{array}$

ここで最後の等式は, 積分領域のコンパクト性から最大値, すなわち有限の値で抑えられることを加味している. この式から, uを原点でTaylor展開した時の1次の項 $\int\int_{B_p} du$ 以外は $p\rightarrow 0$ で消える.

$\displaystyle{|o(p^{-1})\int_0^{2\pi} \cos{t}+\sin{t} dt|}\ (p\rightarrow 0)$

は積分を先に計算する限り0にいくが, 先にpの極限をとると発散する, すなわち収束が一様でないことが気になる. $F(s)=\int_0^{2\pi s} \cos{t}+\sin{t} dt$ は区間 $[0,1]$ を含む開区間上定義された $C^\infty$ 級関数になり, $F(s)=\sin{2\pi s}+1-\cos{2\pi s}\ (s\in (0,1))$ と表される. sが1-pを動くとき,

$|p^{-1} F(s) = -\sin{2\pi p}/p + (1-\cos{2\pi p})/p|\rightarrow 2\pi\ (p\rightarrow 0)$

すなわち最初の式は, 積分区間をパラメータとした2変数(p,s)の関数とみれば, 近づき方により0にも∞にも $2\pi$ のたかだか定数倍にもなるということになる.

まず合成の途中で現れる $G^{-1}$ の形を決める. そのために, 行列 $A\in M_n(R)$ を $End(V)$ の元として $f_A$ とかく時のテンソル表現 $f\otimes w$ を求める. Vの標準基底 $\{e_i \}_{1\leq i\leq n}$ に関する双対空間 $V^\vee$ の双対基底として $\{f_i \}_{1\leq i\leq n}$ をとる. 双対空間 $V^\vee$ の任意の元 $f$ は, 実数列 $\{d_i\}$ で

$f=d_1f_1+\ldots d_nf_n$

と表される. そこで任意の $x\in V;\ x=x_1e_1+\ldots x_ne_n$ は $G(f\otimes w)\in End(V)$ によって,

にうつり, 第j要素について考えるとjを固定したときに動くiに関する和=係数であることが分かり, 線形自己凖同型写像としての行列表現として, iが列, jが行に対応していることが分かる.

すなわち

$Ax=\begin{pmatrix} w_1d_1&w_1d_2 & \cdots & w_1d_n \\ w_2d_1&w_2d_2 & \cdots & w_2d_n \\ \vdots &\vdots && \vdots \\ w_nd_1 & w_nd_2 &\cdots & w_nd_n \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\ \vdots \\ x_n \end{pmatrix}$

$J=G^{-1}\circ F$ は, (i,j)要素が1でそれ以外が0の行列, すなわち行列単位 $E_{ij}$ を $f_j\otimes e_i$ に写す. つまり $J(E_{ij})=f_j\otimes e_i$ .

以下の可換図式を考える.

任意の $A,B\in M_n(R)$ に対し,

Rendered by QuickLaTeX.com

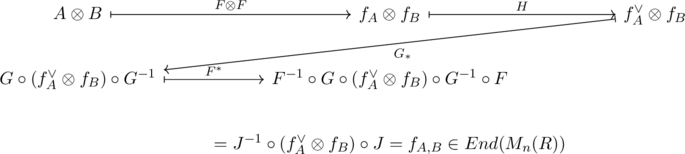
が求める写像の表現である. Jによる行列単位の像は上で計算したとおり $f_j\otimes e_i$ だから, あとは具体的な表示を見るのに $A=(a_1,\ldots,a_n),\ B=(b_1,\ldots,b_n)$ (但し $a_i,\ b_j$ はそれぞれ行列A, Bの第i行, 第j列を表す)とおいて,

$f_{A,B}(E_{ij})=a_j\otimes b_i$

であることが計算で分かる. 任意の行列Xが単位行列の和として

$X=(x_{ij})=\sum_{i,j}x_{ij}E_{ij}$

のように表せることを使うと,

$f_{A,B}(X)=\sum_{i,j}x_{ij}f_{A,B}(E_{ij})=\sum_{i,j}x_{ij}a_j\otimes b_i$

となる(但し $f_j\otimes e_i$ はGによって自然に $End(V)$ の元として見る).
これの積表示は $a_j\otimes b_i=b_i\cdot a_j$ から(この積でn次正方行列ができる), 2次の場合を考えて:

$\begin{array}{lcl} f_{A,B}(X)&=&\sum_{i,j}x_{ij}(b_i\cdot a_j)\\ &=& x_{11}\begin{pmatrix}b_{11}\\ b_{21}\end{pmatrix} \begin{pmatrix}a_{11}& a_{12}\end{pmatrix} + x_{12}\begin{pmatrix}b_{11}\\ b_{21}\end{pmatrix} \begin{pmatrix}a_{21}& a_{22}\end{pmatrix} \\ &+& x_{21}\begin{pmatrix}b_{12}\\ b_{22}\end{pmatrix} \begin{pmatrix}a_{11}& a_{12}\end{pmatrix} + x_{22}\begin{pmatrix}b_{12}\\ b_{22}\end{pmatrix} \begin{pmatrix}a_{21}& a_{22}\end{pmatrix} \end{array}$

から, 各要素を比較して,

$f_{A,B}(X)=BXA$

を得る. この表し方はn次元でも正しい.

次に超越拡大体上のガロア拡大を考察する.
複素数体C上の1変数有理関数体を $K=C(S)$ とおき, LをK上の多項式

$F(x)=x^2-S$

の最小分解体とする. Fの根は $\pm \sqrt{S}\notin K$ を満たす.

( $\sqrt{S},\ S$ )は2変数多項式 $F(x,y)=x^2-y$ があるのでC上代数従属で, LはKに $\sqrt{S}$ を添加して得られる体だから, LのK線形独立基として $1,\ \sqrt{S}$ をとれる(このときのK係数はK上体の演算で生成されるもの, すなわちSを含む有理式である). したがって $[L:K]=2$ .

この考察を元に, 次の問題を考える.

Fの対称性からLは $F^*=x^3-Sx^2+Tx-U$ の根の冪根を添加して得られる. 従って $F^*$ の簡略化を行うために, $F^*$ に変数変換 $x\rightarrow x-(-S/3)$ を施して, $G(x)=x^3+(T-S^2/3)x-S^3/9+ST/3-U=x^3+Vx+W$ を解く. 変数変換を考慮に入れて, $G(x)$ の根を $\{\alpha_i\}\ (i=1,2,3)$ とすれば, $\sqrt{\alpha_i+S/3}$ がKに添加すべき根である.

Lagurangeの方法を使い, 計算は省略するが, 判別式は $Disc(G)=-4V^3-27W^2$ . V, W, Disc(G)はいずれも(S, T, U)のたかだか多項式で生成されるので, $V, W, Disc(G)\in K$ に注意しておく.

$u = \displaystyle{{}^3\sqrt{ \frac{-27W+\sqrt{-27Disc(G)}}{2} }}$
$v=-3V/u,\ \zeta=e^{2\pi i/3}$

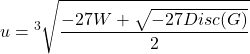
と置き, Gの3根はV, Wにより

$\begin{array}{c} \alpha_1=\alpha=\frac{u+v}{3} \\ \alpha_2=\beta=\frac{\zeta u+\zeta^2 v}{3} \\ \alpha_3=\gamma=\frac{\zeta^2 u+\zeta v}{3} \end{array}$

と表される. 根と係数の関係α+β+γ=0と, 一般にはγは0ではないことを踏まえて, $\sqrt{\alpha+S/3},\ \sqrt{\beta+S/3}$ はK上代数的独立. 同様に $M=K(\sqrt{\alpha+S/3},\sqrt{\beta+S/3})$ 上 $\sqrt{\gamma+S/3}$ が代数的独立である( $\gamma=\pm i\sqrt{\alpha+\beta+S}$ である).

以上から

$L=K(\sqrt{\alpha+S},\sqrt{\beta+S},\sqrt{\gamma+S})$

K上の拡大次数を求めるのに, まず中間体 $M_1=K(u)$ を考える.
uは $u=\zeta^k u \ (k=0,1,2)$ と複素数の中で3つの場合が起こりうるが, k=0として一般性を失わない. $(2u^3+27)^2+27Disc(G)=0$ だから, この左辺のuをxと置き換え, 辺辺4で割ったものがuのK上の最小多項式になる. これは分数次数の文字を含む有理式が体の演算で生成されない ( $\sqrt{-27Disc(G)}\notin K$ )ことと, 多項式の作り方からK上既約かつモニックで, $[M_1:K]=6$ がいえる. $v=-3W/u$ から, $M_1=K(u,v)$ であることも分かる.

次いで $M_2=M_1(\sqrt{\alpha+S})/M_1$ の $M_1$ 上の拡大次数を求めるが, これは $\sqrt{\alpha+S}=\sqrt{3}^{-1}\sqrt{u+v+S}$ から, $\sqrt{u+v+S}$ の $M_1$ 上の最小多項式を求めることと同値. 形から直ちに $x^2-u-v-S$ が目的のものを与えることが分かり, $[M_2:M_1]=2$ . 同様の考察がβ, γに関しても適用され(つまり最小多項式としてそれぞれ $x^2-\zeta^{k_1}u-\zeta^{k_2}v-S\ ((k_1,k_2)=(1,2),(2,1))$ がとれる),

$[L:K]=[M_4:M_3][M_3:M_2][M_2:M_1][M_1:K]=2^3*6=48$

すなわち48次拡大であることが言える.

6次拡大 $M_1/K$ がガロア拡大であることを言う.
まずuをK上の生成元として固定し(vの場合もありうるが), $K$ は標数0の体であるから完全であり, K上のuの最小多項式が既約であるからK上分離的でもあるので, その最小分解体がガロア拡大体であるから, それが $M_1$ に等しいことを言えば良い. 上で議論したとおり, K上の多項式

$\phi_u(x)=x^6+27x^3+27/4(27+D)\ (D=Disc(G))$

はuのK上の最小多項式であり, $M_1$ がその最小分解体に等しい.
それを見るのに $\phi_u$ の $M_1$ 上の分解:

$\phi_u(x)=(x-u)(x-\overline{u})(x-\zeta u)(x-\overline{\zeta u})(x-\zeta^2 u)(x-\overline{\zeta^2 u})$

を考えれば, (1) $\phi_u$ が既約であること $\Leftrightarrow \phi_u$ の根がいずれもKに属さない; (2) $M_1$ がK上 $\phi_u$ の根で生成されること $\Leftrightarrow u^3=\frac{27}{4}(27-D+\sqrt{27D})$ より, $\overline{u}$ が $M_1$ 上代数的に(つまりuを含む有理関数で)生成される

ことにより,

$\begin{array}{lcl} Gal(K(u)/K)&=&\{u,\overline{u},\zeta u,\overline{\zeta u},\zeta^2 u,\overline{\zeta^2 u}\} \\ Gal(K(v)/K)&=&\{v,\overline{v},\zeta v,\overline{\zeta v},\zeta^2 v,\overline{\zeta^2 v}\} \end{array}$

等が分かる. 右側の集合は最初の元の写り先を $Aut_K(M_1)$ の元と同一視したものとして見る. 写り先が $Aut_K(M_1)$ の元を一意に決定するのは, ガロア群のガロア拡大を与える(モニックな)分離多項式の根の集合への作用がtransitiveなことから言える. また上の結果から, ガロア群を与える分離多項式の一つの根zが与えられたとき, 実軸に関する鏡影 $z\mapsto \overline{z}$ および120度の回転 $z\mapsto \zeta z$ という二つの作用の組み合わせでガロア群が構成され, その固定体として $M_1$ の任意の元, 特にuの有理式が不変であることが見れる.

いよいよ3つ目の問いについて考えてみる. $L/K$ がガロア拡大とあるが, それはまだ示していないことなので, 次の補題を示すことで直ちに従うようにする.

補題. Kは標数0の体で, 包含関係 $L\supset M\supset K$ を満たす体の列に対し, $L/M,\ M/K$ は有限次ガロア拡大であるとする. このとき $L/K$ はガロア拡大である.

証明. ガロア拡大が正規拡大でありかつ分離拡大であるという事実を使う. まずガロア拡大M/K, L/Mを与える分離多項式 $f_M,\ f_L$ を, 次のように構成する. Kの代数閉包 $\overline{K}$ から有限個の元 $\{\alpha_i\}\notin K$ を選んで $M=K(\alpha_1,\ldots,\alpha_n)$ となるようにできる. 同様にMの代数閉包 $\overline{M}$ から有限個の元 $\{\beta_i\}\notin M$ を選んで $L=M(\beta_1,\ldots,\beta_m)$ とする. $\alpha_i$ のK上の最小多項式を $\phi_i$ , $\beta_i$ のM上の最小多項式を $\psi_i$ とし, 各々の最小多項式の列の最小公倍数を $\phi,\ \psi$ とすれば, それぞれM/K, L/Mを最小分解体とする分離多項式になる. M/Kは正規拡大であるから, $\phi$ はM上一次式の積に分解するので, より大きな体である $M(\beta_1,\ldots,\beta_m)/K=L/K$ 上ももちろん一次式の積に分解する. $\psi$ もL上一次式の積に分解するから, $\phi\psi$ は $L=K(\alpha_1,\ldots,\alpha_n,\beta_1,\ldots,\beta_m)$ で一次式の積に分解する. $\alpha_i,\ \beta_i$ の取り方から $\phi\psi$ はK上既約であるし, Kが完全体だから分離的であることも言える. 故にLはK上のガロア拡大である.

ちなみに, 標数0の体Kの2の巾次数の拡大はガロア拡大である. なぜならL/Kがそのような拡大体とすれば, LのK上の線形基として $\{1,a\}\ a^2\in K$ を満たすものがとれるので, aの最小多項式がK上の既約分離多項式 $f=x^2-a^2$ と一致する. その最小分解体がLであることは明らかである. 帰納法でLの上のL(b), L(b)の上のL(b,c)を考えることで, 2の巾次数の拡大はガロア拡大である.

話を問いに戻して, L/Kがガロア拡大だということは分かった. $Gal(L/K)$ の位数3の部分群はGの根 $X=\alpha$ を

を推移させる巡回群である. 故に $(X-Y)(Y-Z)(Z-X)$ は3次多項式Gの根を変数とみた差積そのものであり, 判別式の平方根である. 故に $M=K(\sqrt{Disc(G)})$ で, $\sqrt{D}$ は最小多項式 $x^2-D\in K[x]$ を持つから $[M:K]$ =2. 2次拡大はガロア拡大である.

コメントする