写像の文脈では, 著者によって「写す」と「移す」という異なる表記があるらしい. 前者はmapの和訳通り, 「ある集合の元をある集合の唯一つの元に移すもの」, つまり「写像主体」になっていることを強調する表現で, 後者は元そのものが移動する, あるいは移動させるというニュアンスから, 元の集合(domain)と行き先の集合(codomain)に初めから何らかの関係があり, その関係を記述するものが写像である, という「集合主体」の表現であると解釈できなくもない.
最近順系の普遍性がよく分かってきた. その経緯で関連した命題を記しておく.
命題2.8.2: Bが平坦A-代数でかつNが平坦B-加群ならば, NはA-加群として平坦である.
証明: A加群の完全列![]() をとる. このときBは平坦A加群として関手
をとる. このときBは平坦A加群として関手![]() で写される完全列
で写される完全列
![]()
を引き起こす(右完全性は左随伴関手としての![]() の性質により従う).
の性質により従う). ![]() は写像
は写像![]() によりB-加群と見れる. このとき平坦B-加群Nの性質から関手
によりB-加群と見れる. このとき平坦B-加群Nの性質から関手![]() でB-加群としての完全列
でB-加群としての完全列
![]()
が誘導される. 同型![]() によってNのA-平坦性が出る((A,B)-複加群としてのNの性質から, 自然な同型
によってNのA-平坦性が出る((A,B)-複加群としてのNの性質から, 自然な同型![]() を使っている) ■
を使っている) ■
命題2.10: Aを可換環, aをAのイデアルで![]() を満たすものとする(rad(A)はAのJacobson根基). MをA-加群, Nを有限生成A-加群とし,
を満たすものとする(rad(A)はAのJacobson根基). MをA-加群, Nを有限生成A-加群とし, ![]() をA-凖同型写像とする. このとき誘導された凖同型
をA-凖同型写像とする. このとき誘導された凖同型![]() が全射ならuも全射である.
が全射ならuも全射である.
証明: NのA上の生成元を![]() とする.
とする. ![]() が全射であれば, 各生成元
が全射であれば, 各生成元![]() に対し, Mの元で,
に対し, Mの元で, ![]() の
の![]() における像に写すような
における像に写すような![]() が少なくとも一つ存在する. 正確には
が少なくとも一つ存在する. 正確には![]() より
より![]() .
.
そこで
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} \mu(m_i)&=& \nu_i + \sum_j c_{ij}\nu_j \\ &=& \sum_j (\delta_{ij} + c_{ij})\nu_j \\ &=&(c_{i1},\ldots,c_{ii}+1,\ldots,c_{in}) {}^t(\nu_1,\ldots,\nu_n) \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-02b44b6b2ae68f8ba33da6385ac19f1e_l3.png)
より, ![]() と書くことにすれば,
と書くことにすれば,
![]()
とかける. ここで![]() は行列
は行列![]() に対し
に対し![]() で定義されるNの自己凖同型環
で定義されるNの自己凖同型環![]() 上の行列と見る.
上の行列と見る.
![]() の行列式dは
の行列式dは![]() から分かるように, Cの特性方程式に-1を代入したものを
から分かるように, Cの特性方程式に-1を代入したものを![]() 倍したもので,
倍したもので, ![]() の形である.
の形である. ![]() の余因子行列
の余因子行列![]() を(e)の両辺にかけると,
を(e)の両辺にかけると, ![]() を得る.
を得る. ![]() は
は![]() の要素の(n-1)次多項式であるから勿論Aの元.
の要素の(n-1)次多項式であるから勿論Aの元. ![]() であるから
であるから![]() で,
で,
![]()
がMからNへの全射を与えている ■
命題13. ![]() を環凖同型, NをB加群.
を環凖同型, NをB加群. ![]() によってNをA-加群とみてB-加群
によってNをA-加群とみてB-加群![]() をつくる. このときyを
をつくる. このときyを![]() に写す凖同型写像
に写す凖同型写像![]() は単射であること, またg(N)は
は単射であること, またg(N)は![]() の直和因子であることを示せ.
の直和因子であることを示せ.
証明. gの単射性: gはA加群の凖同型であるから, ![]() を言えば良い. 実際
を言えば良い. 実際![]() なら単元
なら単元![]() が存在してay=0より直ちにy=0. なお, ここで単元の存在を言うのは, 0でないyに対してyを零化するAの元の存在を否定できないから. 単元がそのような元である心配はない.
が存在してay=0より直ちにy=0. なお, ここで単元の存在を言うのは, 0でないyに対してyを零化するAの元の存在を否定できないから. 単元がそのような元である心配はない.
また, ![]() は明らかに全射である.
は明らかに全射である.
![]()
このB-加群の列は完全で, pの右逆凖同型, つまりpの分解B-凖同型としてgをとれる. 実際
![]()
で![]() である. 故に
である. 故に![]() は分裂し,
は分裂し, ![]() ■
■
命題. 有向集合Iを固定し, この上のA-加群の順系![]() を考える. 各順系の順極限を
を考える. 各順系の順極限を![]() , 対応する準同型を
, 対応する準同型を![]() とする.
とする.
準同型![]() が図式
が図式
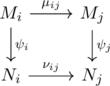
を可換にするとき, 図式(*)
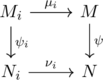
を可換にする準同型![]() が一意的に定義される.
が一意的に定義される.
証明. 示すべきことは次の三つである.
(i) ![]() が写像としてwell-definedであること
が写像としてwell-definedであること
(ii) ![]() が存在すること(手順を与えて構成できる)
が存在すること(手順を与えて構成できる)
(iii) (*)を可換にするような写像として, ![]() が一意的であること
が一意的であること
(i)は(ii), (iii)を示せば明らかであるから, (ii)をまず示す.
加群の直和![]() に対し, 写像
に対し, 写像
![]()
は任意の![]() を
を![]() で
で![]() に写す写像として自然に定義され,
に写す写像として自然に定義され, ![]() である. これは明らかにA-加群の性質を保存する.
である. これは明らかにA-加群の性質を保存する.
このとき(*)の可換性を使えば, 図式
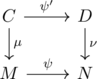
を可換にする![]() として定義できる.
として定義できる.
具体的には![]() に対し
に対し![]() をとり, 次の等式を得る(
をとり, 次の等式を得る(![]() はIの部分集合).
はIの部分集合).
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} (\nu\circ \psi')(x+y) &=& \nu\Big( \sum_{i\in J_1} \psi_i(x_i)+ \sum_{i\in J_2} \psi_i(z_i)-(\psi_j\circ \mu_{ij})(z_i) \Big) \\ &=& \nu\Big ( \sum_{i\in J_1} \psi_i(x_i)+ \sum_{i\in J_2} \psi_i(z_i)-(\nu_{ij}\circ \psi_i)(z_i) \Big) \\ &=& \sum_{i\in J_1} (\nu_i\circ \psi_i)(x_i)\ \ldots \ (*2) \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-be5dd4a82047f79b031e1813a02c38b5_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} (\psi\circ \mu)(x+y) &=& \psi\Big( \sum_{i\in J_1} \mu_i(x_i) \Big) \\ &=& \sum_{i\in J_1} (\psi\circ \mu_i)(x_i)\ \ldots \ (*3) \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-9ea2d3234799977a5a274b90d2912a77_l3.png)
(*2)=(*3)のとき, ![]() を満たす準同型
を満たす準同型![]() を
を
![]()
と定義できる. 但しこの![]() は,
は, ![]() を満たすような
を満たすような![]() が必ず存在するので, そのようなもので任意の一つを取る. 二つの異なる有向集合の元
が必ず存在するので, そのようなもので任意の一つを取る. 二つの異なる有向集合の元![]() で
で![]() を満たすものに対し, (*2)=(*3)によって値
を満たすものに対し, (*2)=(*3)によって値![]() は一意的に定まることがわかる. これで(ii), (iii)が示された. ■
は一意的に定まることがわかる. これで(ii), (iii)が示された. ■