集合論再考 – 解析タネル

Bourbakiの構造論で言うThe Mother Structureの一つ, 順序について考察しました.

自然数μとνの積μνとは:

μをν回足すこと
νをμ回足すこと

有名な掛け算の順序問題ですね。少し前、どちらが合理的か、という問題が議論されました。

個人的にはーどちらの立場を取るか教える段階になってみないと分かりませんがー小学校の先生が教えるということを考慮すれば、各先生方が持っている積の順序の概念の修得を重く見る向きは、多少お節介というか、杞憂ではないのかと考えるわけです。

無論自然数の掛け算とはいっても、順序数の積にまで一般化されれば話は違います。順序数というのは自然数を数の比較可能性と整列性という性質に基づいて拡張したもので, 1からnまでの数の集合を順序数nとして定義したものと考えてとりあえず差し支えはありません(但し「飛び」が許され、 $\{1,\ldots,n\}\cong \{1,3,4,\ldots,n+1\}$ です)。

この順序数にまで抽象化された自然数を考える上で, 掛け算の順序が可換ではないのです。例を挙げましょう。

$\mathbb{N}_i\ (i=1,2)$ を自然数 $\mathbb{N}$ と順序同型(つまり順序数 $\aleph_0=\omega$ の整列集合)とします. 順序同型 $f_\lambda:\mathbb{N}\cong \mathbb{N}_\lambda$ が存在し,

$U_1=\mathbb{N}_1\cup \mathbb{N}_2,\ U_2=\bigcup_{\lambda\in\mathbb{N}}\{1,2\}_\lambda$

とおけば, 順序数の積の定義により,

$${\rm ord}U_1=\omega 2,\ ${\rm ord}U_2=2\omega$

です. これらが一致しないことは以下のようにして確認できます.

$f:\{1,2\}\times \mathbb{N}\rightarrow U_1;\ f(\lambda,x)=f_\lambda(x)$ が $U_1$ の順序同型を与えるので, ${\rm ord}U_1=\omega 2 = \omega+\omega>\omega$ .

一方 ${\rm ord}U_2=2\omega=2+2+\ldots=\omega$ (2015/01/17).

$2\omega$ は $\omega 2$ より真に~~大きい~~小さい順序数となります (2015/01/17)。

この積の定義では、(1)が正当化され、(2)は却下されます。

とはいえ、これを見越して伊藤武広先生のように、小学校の先生に加群や環の素養を課すべきというのは違和感がありますが。

集合はものの集まりですが、構造論の思想としては集合と集合の間に対応を考えるというのが基本的なところである、と書いてあるのを見ました(確か数学でない論文です)。代数、順序、位相どのThe Mother Structuresをとっても「集合」とその間の「関係」の公理が存在しますから、その「関係」を保ったまま別の元に移すものの性質というのは極めて興味深い対象になって自然なことです。

Aの部分集合の個数は？

この答えが $2^N$ (NはAの元の個数)であることは、集合間の写像の個数を使って簡潔に説明されます.

すなわち, Aの部分集合Sを任意にとるとき, 各Aの元がSに含まれるか含まれないかに応じて1か0を割り振る対応 $f_S$ を考えれば、これはAから2点集合{0,1}への写像になります. $f_S\neq f_S'\Leftrightarrow S\neq S'$ なので, 部分集合とこのような写像が1対1に対応し,

部分集合の個数=Aから2点集合への写像の個数

が分かったところで次の命題に帰着します.

命題. ${\rm card}A=n,\ {\rm card}B=m$ を満たす集合A, Bがあるとき, AからBへの写像全体の集合 ${\rm Map}(A,B)$ の濃度は $m^n$ である.

証明. Aの元一つを固定するとき, (空ではない)Bの元を選ぶ方法はm個. 一つの固有な写像 $A\rightarrow B$ を定めることは, Aの全ての元に対しこのような選択の方法を与えることに等しい. 故に $|{\rm Map}(A,B)|=m^n$ (証明終)

以下は最初の方に述べた順序数の性質で特に重要なものです.

命題. 順序数の成す集合は整列集合である
証明. Sを全ての順序数の成す集合とし, 部分集合 $S_\mu=\{\ \nu \in S: \nu<\mu \}$ を考える. ${\rm ord}A=\mu$ となる整列集合Aをとると,

$\nu\in S_\mu \Leftrightarrow \exists a\in A,\ \nu={\rm ord}(A<a>)$

が成立する.

※但しここでの同型は順序同型で, A＜a＞とはa切片のこととする. また後半の主張は整列集合の比較定理により, 順序数が同じでない二つの整列集合は一方の切片と順序同型であることによる.

そこで, 順序数 $\nu\in S_\mu$ を一つ決めることと $\nu={\rm ord}(A<a>)$ となる $a\in A$ を決めることは1対1に対応し, 逆に相異なる $a,\ b\in A$ に対応する切片の順序数は異なるから, $a\in A$ に応じて $\nu\in S_\mu$ が一意的に定まる. この写像は $\omega(a)={\rm ord}A<a>$ と書かれるわけだが,

———————-

順序単射であること
$\begin{array}{l} \forall a,\ b\in A;\ a\leq b\Rightarrow \omega(a)\leq \omega(b) \\ \forall a,\ b\in A;\ \omega(a)\leq \omega(b) \Rightarrow a\leq b \end{array}$
全射であること
A＜a＞に対し常にaをとれるから明らかである.

———————-

により $\omega$ は順序同型. ゆえに $S_\mu\ (\forall \mu\in S)$ は整列集合.

今Sの空でない部分集合Tから任意の順序数 $\nu\in T$ をとるとき, $\nu\leq t(\forall t\in T)$ ならもちろん ${\rm min}T=\nu$ であるし, $\exists t\in T,\ t<\nu$ なら, $T_\nu=S_\nu\cap T$ が整列集合 $S_\nu$ の部分集合で, これはもちろん整列集合であるから(*1), ${\rm min}T_\nu$ がTの最小元を与える. よってSは整列集合である (証明終).

Zermeloの整列定理. Aを任意の集合とするとき, Aに適当な順序≦を定義して(A,≦)を整列集合にできる.

以下ではZornの補題を既知のものと仮定する.

証明. Aの部分集合Wとそこで定義された順序Oとの組, (W,O)が整列集合となっているもの全体を $\mathfrak{M}$ とおく. Aの部分集合として任意の一元集合 $\{a\}$ とそれによって一意的に定まる順序は明らかに整列集合で, $(\{a\},O)\in \mathfrak{M}$ であるから $\mathfrak{M}$ は空でない. 以下では $\mathfrak{M}$ が帰納的順序集合であることを示し, その上に定まる順序に対する極大元として(A,O)がとれることを示す.

$(W,O)\rho (W',O')$ であるとは,「W=W’かつO=O’」または「 $W\cong W'<\nu>\ (\exists \nu\in W')$ 」であると定義する

反射律: W=WかつO=Oであるから明らか.
反対称律: (W,O)ρ(W’,O’), (W’,O’)ρ(W,O)を仮定する. W=W’かつO=O’であるときは問題ない. W≠W’とする. このときWはW’の, W’はWのある切片と順序同型であるが, Wの切片の順序数はWの順序数より真に小さく, W’についても同様. このようなことは起こり得ないので, W=W’. ρの定義からO=O’でもないといけない.
推移律: (W,O)ρ(W’,O’), (W’,O’)ρ(W”,O”)を仮定する. W=W’=W”かつO=O’=O”のときは問題ない. W=W’＜a’＞かつW’=W”＜a”＞のとき, 順序同型f:W=W’＜a’＞, g:W’=W”＜a”＞が存在する(a∈W, a’∈W’, a”∈W”). このときW=W”＜g(a’)＞であることが次のようにして示される. g(a’)∈W”＜a”＞(a’∈W’)からg(a’)＜a”＞. そこで 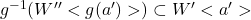$g^{-1}(W''<g(a')>)\subset W'<a'>$ . またgのW’＜a’＞への制限写像をもgと書くとき, 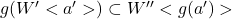$g(W'<a'>)\subset W''<g(a')>$ . ∴ (W,O)ρ(W”,O”) (面倒なことしてますが, 頭のいい皆さんなら切片の定義からa’∈W”と見做せるので, W”＜a’＞=W’＜a’＞=Wでいいだろ！と突っ込むとこですよ). W=W’＜a’＞かつW’=W”や, W=W’かつW’=W”＜a”＞のときは等しくない一方の整列集合の切片への順序同型が存在するのが仮定であるから明らかであろう.

以上のことから, $(\mathfrak{M},\rho)$ は順序集合である. $\mathfrak{N}$ を $\mathfrak{M}$ の任意の空でない全順序部分集合とする.

$W^*=\bigcup_{(W,O)\in\mathfrak{N}} W$

とおくとき, この集合に次のように整列順序 $O^*$ を定義できる.

$\mathfrak{N}$ は全順序部分集合だから, 任意の2元(W,O), (W’,O’)は順序ρで比較可能である. $W^*$ の定義からW=W’の場合は同一と考えれば, 任意の相異なるW, W’の一方は他方の切片になっている. このとき $\forall x,y\in W^*,\ \exists (W,O)\in\mathfrak{N},\ x,y\in W$ だから, この順序OにおいてxOyかyOxかに従ってx≦yかy≦xと定めれば, この順序は(W,O)のとり方によらず一定で, $(W^*,O^*)$ は整列集合となる. しかも任意の $(W,O)\in \mathfrak{N}$ は $(W^*,O^*)$ と一致するかその切片となるので, $(W,O)\rho (W^*,O^*)\ (\forall (W,O)\in \mathfrak{N})$ であることと, $(W^*,O^*)\rho (W,O)$ となるような $(W,O)\in \mathfrak{N}$ があるとすれば, (定義から) $(W^*,O^*)$ でないといけないので ${\rm sup}\mathfrak{N}=(W^*,O^*)$ .

Zornの補題より, $(\mathfrak{M},\rho)$ には極大元 $(W_0,O_0)$ が存在するが, 実は $W_0=A$ である. もし $W_0\neq A$ なら, $A-W_0\ni a$ が存在し, $W_0$ の最後にaを付け加えた集合 $W_1=W_0\cup \{a\}$ に順序 $O_1=O_0+a$ を定義してやればよい. 順序 $O_1$ は $x\O_1 a\ (\forall x\in W_0),\ O_1|W_0=O_0$ を満たすと定義すれば, これは順序ρで $(W_0,O_0)$ より真に大きな整列集合になるので, $(W_0,O_0)$ の極大性に矛盾する(証明終).