holomorphic function germsによるcovering

Riemann Surface $X$ と, 有理型関数体上の $n$ 次既約多項式 $P\in \mathcal{M}(X)[T]$ が与えられたとき, $X$ のbranched holomorphic $n$ -sheeted coveringとなる新しいRiemann Surface $Y$ が同型を除いて一意的に得られる. すなわち対応

$(X,P)\mapsto (Y,\pi,F)$

があり, $(Z,\pi',G)$ も $(X,P)$ から得られた同様の性質を満たすalgebraic functionとする. そうすると図

Rendered by QuickLaTeX.com

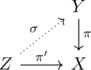
を可換にするbiholomorphic mapping $\sigma:Z\to Y$ がただ一つ存在する.

${\rm Deck}(Y/X)\cong {\rm Aut}_{\mathcal{M}(X)}(\mathcal{M}(Y))$

が群の同型となり, covering map $\pi:Y\to X$ がGaloisであるとき, またその時に限り ${\rm Aut}_{\mathcal{M}(X)}(\mathcal{M}(Y))$ がGalois群になる.

この新しいRieman Surfaceの構成¹^[1]p.54に詳しく書かれてありますが, 特に重要だと思うので概略を書いておきます.

1. 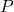$P$ の判別式のpoles, branch points, 及びzerosを除く;

判別式 $\Delta=\Delta(x)\in \mathcal{M}(X)$ は $X$ 上の有理型関数である. また, poles, branch points, zerosは合わせて有限個である. いずれか一つでも無限個あれば, Riemann Surface上の有理型関数に対する一致の定理, $P$ の既約性に矛盾する.

2. それらを除いた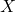 $X$ の部分集合を 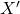$X'$ とする;

この上での多項式

$p_x(T)=T^n+c_1(x)T^{n-1}+\ldots+c_n(x)\in C[T]$

がdistinct $n$ zerosを持つ. この状況において, $P$ は $x$ における $n$ 個のholomorphic function germs $\{\phi_\nu\}\subset \mathcal{O}_x$ を根に持つ¹(Cor.8.8). 従って

$P(T)=\prod_{v=1}^n(T-\phi_\nu)$

と書ける. 同じことだが, $x\in U\subset X'$ なる十分小さい開近傍 $U$ に対し $\{f_\nu\}\subset \mathcal{O}(U)$ が存在し,

$P(T)=\prod_{v=1}^n(T-f_\nu)\ over\ U$

と書ける. これらは局所的な話で, 定義から同じものである. 実際 $x\in U,V,\ f\in \mathcal{O}(U),\ g\in\mathcal{O}(V)$ に対し,

$f=g\ in\ \mathcal{O}_x\Leftrightarrow \exists W\subset U\cap V\neq \emptyset,\ f|_W=g|_W$

である.

3. 最後に

$Y:=\Big\{ \phi\in\mathcal{O}_x : x\in X',\ P(\phi)=0 \Big\}\subset |\mathcal{O}|$

がholomorphic functionsのsheafが誘導する位相に関してhausdorffであって, $P$ の既約性から連結性, 及び $X$ から誘導される複素構造によってRiemann Surfaceとなる. $\pi:Y\to X$ は通常のprojectionとしてn-sheeted holomorphic coveringとなる.

$(X,P)$ からこうして得たRiemann Surface $(Y,\pi,F)$ のことを, ¹では多項式 $P$ から得られた代数関数と呼んでいる.

今 $(X,P)$ から $(Y,\pi,F)$ が得られているとして, $K=\mathcal{M}(X),\ L=\mathcal{M}(Y)$ とおくと, 体の拡大

$\pi^*:K\hookrightarrow L;\ f\mapsto f\circ \pi$

がある. しかも $\exists (f,x)\in K\times X\ s.t.\ \ y,y'\in \pi^{-1}(x),\ y\neq y',\ f(y)\neq f(y')$ のとき, この拡大次数は $n$ である.

Riemann Surface上の有理型関数体の拡大次数に関する最後のステートメントは, Riemann Surfaceの間のbranched holomorphic n-sheeted covering map $\pi:Y\to X$ に成立する事実で, 主張として次の3つに分割できる(証明はここではしないが, ¹Theorem. 8.3参照).

(i) $L=\mathcal{M}(Y),\ K=\pi^*\mathcal{M}(X)$ と置くとき, $L/K$ は代数拡大である.
(ii) $f\in L$ で最小多項式 $f_0$ の次数が最大であるものをとると, $L=K(f_0)$ . しかも $deg(f_0)=n$ .
(iii) $deg(f_0)=m<n$ とする. このとき, 各点 $x\in X$ と $y_j\in\pi^{-1}(x)$ に対し, $f_0(y_i)\neq f_0(y_j)\ (i\neq j)$ なるファイバーの点の個数は $m$ を超えない.

一般の複素関数論におけるWeierstrassの予備定理は, 全ての座標について正則であって, 一つの複素座標 $w$ に関して正常かつモニックな多項式 $F$ が, 基本対象関数が正則であるような正則関数, distinguished polynomialと, 十分小さい多重円板の上で零とならない正則関数の積に一意的に表されることを主張する.

その多重円板での根を $z$ の関数として $w_j(z)$ と表すとき, これらは一般には正則ではない. 2次元において, 局所的に分数次数変数のbranched meromorphic functionによってこれらが表されるというのがPuiseux expansion (ピュィズー展開)の主張である.

$F(z,w)=w^2-z^3w+z\in C\{\{z\}\}[w]$ をローラン級数体上の多項式とするとき,

(a) $F$ が $C\{\{z\}\}$ 上既約であることを示し, (b) F=0で定まる代数関数のPuiseux expansion (Puiseux expansion)

$w=\sum^\infty_{\nu=0}c_\nu z^{\nu/2}$

を求める. (a)はUFD上の多項式に関するEisensteinの判定により直ちに従う.
判別式 $D(z)=z(z^5-4)$ が零とならない一点 $z_0$ とその近傍 $U_0$ を選んで, $F(z,w)$ が $U_0$ において重根を持たないようにできる. また,

$D_1(w,\alpha):=\{w:|w|<|\alpha|,arg(1-w/\alpha)\in [0,2\pi)\},\ D_2(w,\alpha):=\{w:|w|<|\alpha|,arg(w/\alpha)\in [0,2\pi)\}$

に対し, $D_1(z^5,4)\cap D_2(z^5,4)$ 上logの正則な枝が定義され, 一般二項級数

$\begin{array}{lcl}\frac{\partial}{\partial w}\sqrt{w-\alpha} &=& -\frac{i}{2\sqrt{\alpha}}\frac{1}{\sqrt{1-w/\alpha}} \\&=& -\frac{i}{2\sqrt{\alpha}} \sum_{k=0} \frac{(2k-1)!!}{(2k)!!} (\frac{w}{\alpha})^k\end{array}$

が意味を持つので, 積分定数をCとして積分し,

$C+\int \frac{\partial}{\partial w}\sqrt{w-\alpha}dw = C-\frac{i}{2}\sum_{k=0}\frac{(2k-1)!!}{(k+1)(2k)!!}\alpha^{-(k+1/2)}w^{k+1}$

を得る. $\sqrt{\alpha-\alpha}=0$ から,

$C=\frac{i\sqrt{\alpha}}{2}\sum_{k=0}\frac{(2k-1)!!}{(k+1)(2k)!!}$

を得る. $D_3:=\{0<z<{}^5\sqrt{4} \}$ とおいて, $D_1\cap D_2\cap D_3$ 上,

$\begin{array}{lcl} w(z) &=& \frac{\sqrt{z}}{2} \Big( \sqrt{z}^5 - \frac{i}{2} \sum_{k=0} \big[ \frac{(2k-1)!!}{(k+1)(2k)!!}4^{-(k+1/2)}(z^5)^{k+1} \big] -C \Big) \\&=& -\frac{C}{2}\sqrt{z} + \frac{1}{2}\sqrt{z^6} -i \sum_{k=0} \frac{(2k-1)!!}{(k+1)(2k)!!}4^{-(k+3/2)}\sqrt{z}^{10k+11}\end{array}$

が $F$ の一つの根を与える.

1.
Gilligan B, Forster O. Lectures on Riemann Surfaces. Springer New York; 2012. https://books.google.co.jp/books?id=6wvpBwAAQBAJ

Footnotes[+]

Footnotes
↑1	p.54

1. の判別式のpoles, branch points, 及びzerosを除く;

2. それらを除いたの部分集合をとする;

3. 最後に

1. $P$ の判別式のpoles, branch points, 及びzerosを除く;

2. それらを除いた $X$ の部分集合を $X'$ とする;