体上の有限生成環に関して1

関連する事実・補題について少しまとめた.

デデキント整域の性質

【環Aが整域のとき】

零でないすべての分数イデアルが可逆⇔Aはデデキント整域

【環Aがクルル次元1のネータ整域のとき】

(i) 整閉
(ii) 準素イデアルが素イデアルの積で表される
(iii) すべての商体でない局所環はDVR

prob.9.1. Aをデデキント整域とし, SをAの積閉集合とする. このとき $S^{-1}A$ はデデキント整域かAの商体である.
proof.9.1. Aがデデキント整域なら, Aは次元1のネータ整域であって整閉であるので, $S^{-1}A$ はネータ整域で整閉である. 零でないAの素イデアルp(仮定よりこれは極大)でSと交わらないものは, $S^{-1}A$ の素イデアルと一体一に対応する. 従ってその素イデアル $S^{-1}p$ は $S^{-1}A$ における極大イデアルである. よって ${\rm dim}S^{-1}A=1$ . p=0ならこれは商体と一致する.

全ての商体でない局所環はDVRである. DVRはもちろんデデキント(局所)整域であるから, S= $S_p=A-p\ (p\in {\rm Spec}(A)\backslash \{0\})$ の場合は正しい.

prob.9.1.2 Aをデデキント整域とし, $S\neq A-\{0\}$ , H, H’をそれぞれ $A,S^{-1}A$ のイデアル類群とする. イデアルの拡大は全準同型 $H\rightarrow H'$ を引き起こす.

proof.9.1.2 IをAのイデアル群, Pを単項分数イデアルの成す部分イデアル群, Hをイデアル類群, $I',P',H'$ を対応する $S^{-1}A$ の群とする. JをSと交わりを持つ素イデアルで生成されるIの自由部分アーベル群とする.
イデアルの拡大はイデアル群の間の写像 $I\rightarrow I'$ を定義し, これは( $S^{-1}(I_1I_2)=(S^{-1}I_1)(S^{-1}I_2)$ だから)準同型になる. イデアル群の単位元はデデキント整域自身であるから, $S^{-1}I=S^{-1}A=1_{I'}\Leftrightarrow I\cap S\neq \emptyset$ により, $J\rightarrow I'$ は零写像になる. デデキント整域において任意のイデアルが一意的に素イデアルの積にかけるから, $I/J\cong I'$ である.

$J\subset P$ を示す.
$J=\sum_i^n p_i/s_i\ (s_i\in S,\ p_i\in {\rm Spec}(A)\ p_i\cap S\neq \emptyset)$ と書けるが, $t=\prod_i s_i,\ \alpha=\sum p_i$ とおくと,

デデキント整域におけるガウスの補題

Aをデデキント整域, $f\in A[x]$ を多項式とする. $f=a_0+a_1x+\ldots+a_nx^n$ のとき, $c(f)=(a_0,\ldots,a_n)$ はAのイデアルで $c(fg)=c(f)c(g)$ が成り立つ.

一般に $c(fg)\subset c(f)c(g)$ は言える. なぜなら $\sum_{i,j}(a_ib_j)\subset\sum_i(a_i)\sum_j(b_j)$ が成り立つからである.
逆を言うために剰余環のイデアルとして $c(f)c(g)/c(fg)=0$ が成り立てば良い. これは局所的性質であるから, 任意の極大イデアルmに対し, $c(f)_mc(g)_m/c(fg)_m=0$ を言えば良い.

任意の零でない素イデアルpは極大で, 局所化すると離散付値環 $A_p$ が得られるが, これは全ての非零イデアルが極大イデアルpの冪で表されるようなPIDである. $p=(\omega)_{A_p}\ (\omega\in A_p)$ となるものがあるので, 局所環上でのcontentsを $c_p(f_p)=(a_0,\ldots,a_n)_{A_p}\ (a_j\in A_p,\ f_p\in A_p[x])$ と定義すると, これは単項イデアルであるから $c_p(f_p)=(\omega^k)$ なるkがある. 以降DVRにおけるイデアルが $(\omega^m)$ で表されるとき, その次数mを $\deg(I)$ と書くことにする.

$c_p(g_p)=(\omega^l)$ に対し, $c_p(f_p)c_p(g_p)=(\omega^{k+l})$ .

$c_p(f_pg_p)=\sum_{i,j}(a_ib_j)=(\omega^m)$

となるmは $m=\min\{\deg(a_i)\} + \min\{\deg(b_i)\}=m_1+m_2$ と表される. $m_1,m_2$ に対応してそれぞれ $c_p(f_p),c_p(g_p)$ が定まり, また $m=m_1+m_2$ に対応して $c_p(f_pg_p)$ が定まる. 最小値一意性により, $c_p(fg)=c_p(f)c_p(g)$ ■

Gを位相空間とする.

lemma.10.0 Gの対角線集合が閉集合であることは, Gがハウスドルフ空間であることの必要十分条件である.
pf.10.0 対角線集合を $D=\{(x,y)\in G\times G|x=y\}$ とおく. $G\times G-D$ は開集合だから, $(x,y)\in G\times G-D$ の開近傍 $(x,y)\in U_1\times U_2$ がある. $(x,y)$ の取り方から $x\neq y\ (\forall x\in U_1,\ y\in U_2)$ . つまり $U_i\ (i=1,2)$ はGの相異なる元x, yを分離する開集合を与える■

Gを位相アーベル群とする.

lemma.10.1 HをGにおける0の全ての近傍の共通集合とする. このとき次が成立する.

Hは部分群
Hは 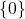$\{0\}$ の閉包
G/Hはハウスドルフ空間
Gはハウスドルフ空間⇔H=0

pf.10.1
(1) 0の任意の近傍Uに対し, $a+U$ はaの近傍を定義する. 逆にaの近傍はこの形のものに限る(平行移動 $T_a(x)=x+a$ は同相 $G\cong G$ を定義する). 故に $x,y\in H$ なら任意の $O,O'\in V(0)$ に対し $x,y\in O,O'$ だから, $x+y\in T_x(O)\cap T_y(O')\subset H$ (xの近傍全部の共通部は0の共通部に含まれる. yも同様である). 同様の記号で, 同相 $x\mapsto -x$ によって $O\cong -O$ が定義される. この写像で0は動かないから, $x\in H\subset O$ なる0の開近傍Oに対し, $-O\ni -x$ はOと同相な0の開近傍である. $O\in V(0)$ は任意だから, $-x\in H$ ■

(2)

$\begin{array}{lcl} x\in \overline{\{0\}} &\Leftrightarrow& U_x^\circ\cap \{0\}\neq \emptyset\ (\forall U_x\in V(x)) \\ &\Leftrightarrow& 0\in U_x^\circ \ (\forall U_x\in V(x)) \\ &\Leftrightarrow& V(x)\subseteq V(0) \\ &\Leftrightarrow& x\in \bigcap V(x)\subseteq H \end{array}$

(3) Hの剰余類g+Hは, 平行移動(同相) $T_g:G\rightarrow G$ によるHの像であり, これはHが閉であるから閉である. 故にG/Hの任意の点は閉集合で, 一点集合が閉である位相群はハウスドルフである.

(4) H=0ならG/H=Gがハウスドルフとなる. 逆にGがハウスドルフなら $x\neq y$ についてx, yを分離する近傍 $U_x,\ U_y$ があるので, 対角線集合 $D\subseteq G\times G$ を除いた $G\times G-D$ の各点はこのような近傍で覆われる. 従って開集合. 故に対角線集合は閉集合. 故に一点集合は閉集合. つまり $\{0\}=\overline{\{0\}}=H$

以下可換位相群Gは, 0に可算近傍系を持つとする(これは可算基本近傍系を持つ第一可算公理よりも強い条件).

コーシー列の同値類は $\widehat{G}$ と書き, コーシー列の和がまたコーシー列になるためには, 任意の $U\in V(0)$ に対し, $x\in U$ なら $x+U\subseteq U$ が必要十分である. 実際 $\{x_\nu\},\ \{y_\nu\}$ をコーシー列とすると, 任意の $U\in V(0)$ に対し整数 $s(U)$ が存在し, $\nu,\mu\geq s(U)$ なら $x_\nu-x_\mu,\ y_\nu-y_\mu\in U$ である. そこで $x_\nu-x_\mu+U\subseteq U$ であれば $x_\nu+y_\nu$ の差がUに入る. $x+U$ はxのある近傍を定義するので, $x+U\subseteq U$ は $V(x)\subset V(0)$ . 上の(2)により, これはH=0, つまりGがハウスドルフであることを要求する.

二つの可換な位相群G, Hと連続な準同型 $f:G\rightarrow H$ が与えられたとき, Gのコーシー列 $\{x_\nu\}$ はfによってHのコーシー列に写る. 実際 $U'\in V_H(0)$ を任意にとったとき, $f^{-1}(U')=U\in V_0(0)$ (fは連続で, 準同型)となるUがある. $s(U)\in Z$ が存在し, $\nu,\mu\geq s(U)$ なら $x_\nu-x_\mu\in U$ となるから, $f(x_\nu)-f(x_\mu)\in f\circ f^{-1}(U')\subseteq U'\in V_H(0)$ となる. よってfは連続な準同型 $\widehat{f}:\widehat{G}\rightarrow \widehat{H}$ を誘導する.

このとき

$G\overset{f}{\rightarrow}H\overset{g}{\rightarrow}K$ なら, $\widehat{g\circ f}=\widehat{g}\circ \widehat{f}$

群の列 $\{A_n\}$ と準同型 $\theta_{n+1}:A_{n+1}\rightarrow A_n$ があるとき, 直積群 $A=\prod A_n$ の写像を $d^A:A\rightarrow A$ を $d^A(a_n)=a_n-\theta_{n+1}a_{n+1}$ と定める(演算は加法的に書いているが, 可換である必要はない).

$d^A(a)=a-(\theta_2a_2,\theta_3a_3,\ldots,\theta_{n+1}a_{n+1},\ldots)$

は準同型である(明らか). そこで ${\rm ker}d^A\cong \displaystyle{\lim_\leftarrow} A_n$ . 3つの逆系 $\{A_n\},\{B_n\},\{C_n\}$ の完全列の可換な図式

Rendered by QuickLaTeX.com

があれば, 準同型の列

が誘導される. 実際直積群の準同型は $f_n:A_n\rightarrow B_n$ に対し, $f:A\rightarrow B$ を $f(a)=(f_1(a_1),\ldots f_n(a_n),\ldots)$ と置くことで定義される. これに対応して準同型

$\pi\circ f: A\rightarrow B\rightarrow \displaystyle{\lim_\leftarrow}B_n\cong B/{\rm Im}d^B$

が定まる.

$\begin{array}{lcl} {\rm ker}(\pi\circ f) &=& f^{-1}({\rm ker}\pi) \\ &=& f^{-1}({\rm Im}d^B)\supseteq {\rm Im}d^A \end{array}$

であれば普遍性によって剰余群の間の準同型が定まる. しかしこれは図式の可換性によって

$f_n(a_n-\theta_{n+1}a_{n+1})=f_n(a_n)-\theta_{n+1}'f_{n+1}(a_{n+1})$

が成り立つので正しい. $\displaystyle{\lim_\leftarrow}B_n\rightarrow \displaystyle{\lim_\leftarrow}C_n$ 間の準同型も同様である.

prop.10.2

$0\rightarrow \{A_n\}\rightarrow \{B_n\}\rightarrow \{C_n\}\rightarrow 0$

を逆系の完全列とすれば,

$0\rightarrow \displaystyle{\lim_\leftarrow}A_n\rightarrow \displaystyle{\lim_\leftarrow}B_n\rightarrow \displaystyle{\lim_\leftarrow}C_n$

は完全列. さらに $\{A_n\}$ が全射的な系ならば

$0\rightarrow \displaystyle{\lim_\leftarrow}A_n\rightarrow \displaystyle{\lim_\leftarrow}B_n\rightarrow \displaystyle{\lim_\leftarrow}C_n \rightarrow 0$

は完全列である.

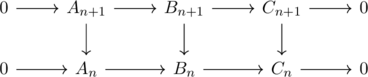
いわゆる「蛇の補題」.

prop.2.10 可換な完全列

Rendered by QuickLaTeX.com

は完全列

Rendered by QuickLaTeX.com

を誘導する.

pf.2.10 a:A→Bをkerfに制限した写像はまた単準同型である. これをpとする. 同様にbをkergに制限した写像をqとする. p(kerf)⊆kerqはすぐに出る(∵(q∘p)(kerf)⊆(b∘a)(A)=0). 逆にy∈kerqならpは単射なので

$\begin{array}{lcl} 0&=&g(y) \\ &=&(g\circ p)(p^{-1}(y)) \\ &=& (p'\circ f)(p^{-1}(y)) \\ &\therefore& f(p^{-1}(y))=0 \\ &\therefore& p^{-1}(y)\in {\rm ker}f \\ &\therefore& y\in p({\rm ker}f) \\ &\therefore& {\rm ker}q\subseteq {\rm Im}p \end{array}$

境界準同型

$d:{\rm ker}h\rightarrow {\rm coker}f$

は, $z\in {\rm ker}h$ に対し, bの全射性から $z=b(y)$ となる $y\in B$ が存在する. 図式の可換性から $0=(h\circ b)(y)=(b'\circ g)(y)$ となり, $g(y)\in {\rm ker}b'={\rm Im}a'$ なので $a'(x)=g(y)$ となる $x\in A'$ がある. xの ${\rm Coker}f$ における像を[x]と書くと, $z\mapsto [x]$ がdを定義し, これは準同型になる.

実際z=b(y)=b(y’)となる $y,y'\in B$ に対し, g(y)=g(y’)=a'(x)なる $x\in A'$ が取れるので, zの取り方によって一意的に[x]が定まる. よってこれはwell-definedである. また $z,z'\in {\rm ker}h$ なら, $z=b(y),\ z'=b(y')$ となる $y, y'\in B$ がとれて, $z+z'=b(y)+b(y')=b(y+y')$ となる. そこで $g(y)=a'(x),\ g(y')=a'(x')$ なる $x,\ x'\in A'$ に対し, $g(y+y')=g(y)+g(y')=a'(x)+a'(x')=a'(x+x')$ . よって $[x]+[x']=[x+x']$ により, これは準同型となる.

残りは省略■

lemma.10.0 ハウスドルフ空間であるような位相群Gが離散位相を持つなら, 完備である.
pf.10.0 $(a_n)$ をGのコーシー列, $(b_n)$ を $(a_n)$ と同値なGのコーシー列とする. $\forall U\in V(0)$ に対し, $\exists s(U)\in Z$ で $\mu,\nu\geq s(U)\Rightarrow a_\nu-a_mu\in U$ を満たす. 離散位相を持つため任意の部分集合, 特に一点集合として取ったUが開集合になるので, $U=\{0\}$ として良い. このとき十分大きなμに対し, $a_\mu=a_{\mu+1}$ となるが, μはUに対し定まる整数であるから有限. つまりGにおいて $(a_n)$ と同値な任意のコーシー列 $(b_n)$ は, ある整数μが存在して $a_\mu=b_\mu$ . これはGが完備であるということである■

環Aから位相環を構成できる.
aをAのイデアル, G=Aを加群としての環A, $G_n=a^n$ , 0の基本近傍系を

$B(0)=\{G_n|n\geq 0\}$

と定義する. このとき0の全近傍系は $V(0)=\{V\supseteq B|B\in B(0),\ V\in S(G)\}$ で与えられる(S(G)はGの冪集合). 平行移動によって任意の0近傍Uはh近傍に写り, 逆にh近傍は $T_h:U\mapsto h+U$ の形で定まる. 従ってこのときGの開集合系は

$\mathfrak{D}=\{O\in S(G) | x\in O\Rightarrow O\in V(x)\}\cup \{\emptyset\}$

で与えられる. 実際この方法で導入された集合系 $\mathfrak{D}$ は一意的に定まり, 確かに開集合系の公理を満たすことが分かる(松坂, p. 163). また積演算 $(x,y)\mapsto xy$ は連続になり, Gは位相環になる. なぜならxyの近傍 $xy+a^n\in V(xy)$ で $(x+b, y+c)\in V(x)\times V(y)$ となる $b,c\in V(0)$ がある(少なくとも $a^n\subseteq b,c$ である. もし $a^n\not\subseteq b$ なら $z\in a^n\backslash b$ がとれて,要素の積がxy+【0の近傍】となるものが, (x+【0の近傍】, y+【0の近傍】)の形のものに限ることに等しい).

整数環において $a=(6)$ とするとき, $a^2=(36)=(9)(4)$ であるから, $xy+a^2$ は $(x+(9),y+(4)),\ (x+a,y+a)$ どちらの積によっても作れる. $a^2\subseteq (9),\ a^2\subseteq (4)$ だから, $(9),(4)$ が0の基本近傍系 $\{a^n\}$ の元を含むので, 0の近傍となっている.

イデアルの既約性と位相空間の既約性について

既約なイデアルとは, 環のイデアルa,b,cに対して $a=b\cap c\Rightarrow a=b\vee a=c$ が成り立つイデアルaの事を言う. これは準素分解の文脈で使われ, ネータ環において全ての既約イデアルが準素イデアルであるという性質がある.

一方で既約な位相空間とは, 空でない位相空間で任意の空でない開集合がその位相空間で稠密であるものを言う.
また既約な位相空間は任意の空でない二つの開集合が交わりを持つとも言い換えられ, (補集合を取ることで)同等の言い換えとして, 台集合Xがどのような二つの真の閉部分集合の和にも分解されないとも言える( $O\cap U\neq \emptyset \Leftrightarrow O^c\cup U^c \neq X\ (\forall O,U\in \mathfrak{D}(X))$ ). またXに対してスペクトラムSpec(X)が位相空間として既約であることと, r(0) (冪零元根基) が素イデアルとなることとは同値である(Atiyah, ex. 1.19).

th.7.14. Hilbertの強零点定理 kを代数閉体, $A=k[t_1,\ldots,t_n]$ (有限生成k代数でも良い)として, $a\subseteq A$ をイデアルとする. $Z(a)\subseteq k^n$ をaによって定義される多様体, I(Z(a))をその多様体を零点として持つAの元全体の成すイデアルとすると, $I(Z(a))=r(a)$ .
pf.7.14.