To give a functor from a category of commutative monoid to the category of abelian group, namely,
![]()
let us construct the abelian group for given ![]() , define
, define ![]() with equivalent relation of
with equivalent relation of
![]()
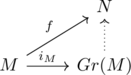
and universal property characterized by the following commutative diagram (for given and constructed monoid homomorphism ![]() and for any monoid homomorphism
and for any monoid homomorphism ![]() , there uniquely exists abelian homomorphism
, there uniquely exists abelian homomorphism ![]() that commutes the diagram).
that commutes the diagram).
By this construction, there’s the identity element ![]() and for each element
and for each element ![]() we have unique inverse
we have unique inverse ![]() and exposes other functorial properties.
and exposes other functorial properties.
To confirm all those properties are valid on this construction, we begin with checking the compatibility of additive operation in the Cartesian product of commutative monoid ![]() and in that of
and in that of ![]() , namely,
, namely,
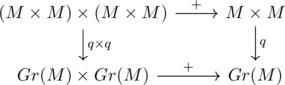
Here q is the quotient map. To verify this, we just show the equation ![]() for any
for any ![]() is valid.
is valid.
Let ![]() represent
represent ![]() respectively. Then the equation above reduces to the equation
respectively. Then the equation above reduces to the equation
![]()
Let ![]() be corresponding elements of M to
be corresponding elements of M to ![]() in such a way that:
in such a way that:
![]() ,
, ![]() and
and ![]() . Set
. Set ![]() and
and ![]() , then we have the equation (*) ■
, then we have the equation (*) ■
With this compatibility, we can immediately verify ![]() .
.
Now define ![]() by
by ![]() . We will now verify the following proposition.
. We will now verify the following proposition.
Prop.
is injective if and only if
has cancellative property, i.e.
Proof.
Suppose M is cancellative, then assumingis equivalent condition to
. Conversely when
is injective, then if there exists a non-cancellative element
for
, i.e.
but
.
being injective can be restated by
, obviously contradict ■
Next let’s show another important property that the Grothendieck construction is idempotent on an abelian group, to be precise, restate in a form of proposition as following.
Prop.
is bijective
Proof.
. Then
s.t.
. k can be canceled and we have
. Put
, then a is the inverse of y.
Let
represents
. We have
. By canceling k, we have
, which indicates
■
Another construction:
We cannot avoid another construction of the Grothendieck group by means of completion of group, because not only of the historical importance, but we can also need this for ring construction for the basis of K-theory.
For given ![]() , denote the free abelian group
, denote the free abelian group ![]() generated by the elements of M as the free basis, in which the element is denoted by
generated by the elements of M as the free basis, in which the element is denoted by ![]() for
for ![]() . Let
. Let ![]() be the subgroup of
be the subgroup of ![]() generated by an element of the form
generated by an element of the form ![]() . We define the quotient group
. We define the quotient group ![]() .
.
Our claim is ![]() .
.
This isomorphism (and the universal property from the former construction) is verified by proving following proposition.
Prop. The properties of free generator constructed Grothendieck group
.
(a)is composed of a form of element
.
(b) For,
Proof.
(a) By expressing the elementas the finite sum
, we can immediately get the equation
And then adding up the differences of generators compose the given form.
(b) When there exists
s.t.
, this is obvious by the cancellation of
. Conversely if
, then
Observing the number of generators of free abelian group of the form
and
, we conclude that we can remove brackets and obtain the results ■
Now consider the following commutative diagram:
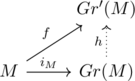
Here ![]() is defined by
is defined by ![]() , and
, and ![]() is defined by
is defined by ![]() .
.
With the previous proposition, we can see ![]() is surjective by (a) and injective by (b), then we have
is surjective by (a) and injective by (b), then we have ![]() .
.
Finally, we’ll view ![]() as a functor. Let A,B be elements of
as a functor. Let A,B be elements of ![]() . For
. For ![]() ,
, ![]() is induced identity in
is induced identity in ![]() because of the uniqueness property:
because of the uniqueness property:
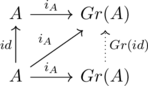
Also the composite property is verified with the uniqueness property by replacing the map and range and extending the diagram above.