連続関数について – 解析タネル

Gluing Lemma:

連続関数族 $\{f_j\}_{j\in I}:A_j\to Y$ が与えられているとする. このとき,

(A) 与えられた(連続とは限らない)関数 $f:\cup A_j\to Y$ が $f|_{A_j}=f_j$ を満たすなら, fは連続である.
(B) 各 $i,j\in I$ について, $f_i|_{A_i\cap A_j}=f_j|_{A_i\cap A_j}$ を満たすなら, 連続関数 $f:\cup A_j\to Y$ で $f|_{A_j}=f_j$ を満たすものが唯一つ存在する.

という二つの性質を考えたい. $\{A_j\}$ が開集合族であるか, $\{A_j\}$ が閉集合族であってIが有限であれば性質(A), (B)は同時に満たされる. (A)が満たされる場合を特にgluing lemmaという. 興味は性質(A)と(B)に違いがあるかということだ.

実はこれらの性質に違いはない.

実際のところ, (A)では関数 $f:\cup A_j\to Y$ で $f|_{A_j}=f_j$ を満たすものの存在を仮定している. これは(B)の仮定を成立させる(さもなくば, 与えられた関数 $f$ がある点 $x\in A_i\cap A_j$ で多価になることを許すが, これは関数の定義に反する). 従って(A)から直ちに(B)が従う. 逆に(B)を仮定すると, (A)の仮定の性質をもつ連続関数 $f$ が構成できる. $f$ と(B)で構成した連続関数 $g$ は異なるかもしれないが, $f$ は $f_i|_{A_i\cap A_j}=f_j|_{A_i\cap A_j}$ を満たし, かつこれは一意性を言ってるので, $f=g$ が分かる. 結局これらの性質は同値になる.

連続関数の族を連続的に拡張させるという試みはもう少し一般的な枠組みで(位相空間論として)100年前の論文に既に現れている.
次の命題はそのような結果の一つで, 元々評価関数 $X\times C(X,Y)\to Y; (x,f)\mapsto f(x)$ が連続になる(= $C(X,Y)$ のCompact-Open topologyがadmissible)ために, Xに幾つかの位相的な性質(例えばある種の有限性)を課す必要が分かっていて, 特にハウスドルフ・コンパクトの場合は都合が良いのでその場合に帰着できることを保証するものである.

先に証明を書いてしまったので英語です.

A: top. sp., $C\subset C(A)$ を連続関数 $A\to A$ の成す集合, $A*$ をAの一点コンパクト化とする.
このとき, C with g-topology and C* with k-topology are homeomorphic.

Pf. Denote A and A* for corresponding base spaces, where A* is the compactification of A and $\phi:C\to C*$ maps $f\in C$ to the unique map $f^*\in C*$ defined by $f^*|_A=f$ and $f^*(I)=I$ . $f^*$ is continuous since for any open set $U*\subset A*$ containing I, the inverse image of $f^*$ is by definition U+I where $+$ denotes the disjoint sum as a set and $U\subset A$ is an open set in A whose complement is compact in A, which is again open in A*.

$\phi$ is homeomorphism is rather trivial since $f^*$ restricts to A coincide f and thus for any subbase element of g-topology in C, namely $W(K, U)\subset (C,g)$ (where $K\subset A$ is closed and $U\subset A$ is open and either K or $U^c$ is compact), $\phi$ maps to an element of k-open subbase $W'(K*, U*)$ , where $K*=K$ is compact in $A*$ because $A*$ is compact and K* is closed　■

Aがlocally compact Hausdorffなら, $C(A)$ のk-topology (Compact Open topology)はadmissibleで, 特にこの構成によって存在が示されたものはadmissible topologyの中で最も粗い(R.F.Arens). Yがlocally compact Hausdorffであるときexponential lawによる以下の関数の間の一対一対応

$X^{Y\times Z}\to (X^Y)^Z; (y,z)\mapsto f(y,z)\leftrightarrow (z\mapsto f(*,z)\mapsto f(y,z))$

により, $f:Y\times Z\to X$ が連続⇔ $\theta:Z\to X^Y; \theta(z)=f(*,z)$ が連続

が分かる. ここでUを $R^n$ のopen ball, $X=Y=\overline{U},\ Z=U$ とすると, Yはlocally compactであるから $X^Y$ がadmissible k-topologyを持つ. $X^Y=C(Y,X)$ のsubspace topologyにより $homeo(Y,X)=homeo(Y)$ の部分集合

$G:=\{f\in homeo(Y) : f|_{\partial \overline{U}}=id \}$

を位相空間と見ると, $G$ は $homeo(Y)$ のstrongly stable subgroupである. strongly stable homeomorphismは $id_{\overline{U}}$ にisotopic(J. W. Alexander, 1923)で, Zと共にGがpath connectedであることにより,

Rendered by QuickLaTeX.com

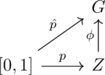
が可換になる. ここでpはZのsmooth path, $\hat{p}$ はGにおけるpathで, Gの元と $id_{\overline{Y}}$ とのisotopyをパラメータ $t\in [0,1]$ の関数と見たものである. $\phi:Z\to G$ は $z\mapsto \theta_z\in G$ で定義され, 特に $\theta_z(z)=z_0$ ( $z_0$ はUのfixed point)を満たすもの(もちろん $Z\to G$ は全く一意的ではないので構成する必要がある. これについてはFadellの本等を参照のこと).

故に $\phi$ は連続である. すなわち $(z,y)\mapsto \theta_z(y)$ は連続(実はこのpath-connectednessを使わなくとも $\phi$ の連続性は言える).