lint – icefog BLOG

良い気候になってきましたな。

先日岡本というところに行って来ました。
なかなかに洒落た町並みで、京都のような大きさや華やかさはないものの、欧風の小道や店舗、カフェが立ち並んで小さな神戸という雰囲気が漂っていました。

今日も普段気になった内容について構成を追ってみたり、具体例を吟味して解説しています。

—————————————–

Proposition: 可換環R上の対称式 $f(t_1,\ldots,t_n)\in R[t_1,\ldots,t_n]$ が与えられたとき, 多項式 $g(T_1,\ldots,T_n)\in R[T_1,\ldots,T_n]$ で

$f(t_1,\ldots,t_n)=g(s_1,\ldots,s_n)$

を満たすものを作るアルゴリズムを記述せよ.

Proof: 構成は [中島匠一, 代数方程式とガロア理論)] に倣った. 存在の証明もそちらを参照されたい.
まず $\hat{f}(t_1,\ldots,t_{n-1})=f(t_1,\ldots,t_{n-1},0)$ は(n-1)変数多項式で, (n-1)変数基本対称多項式によって,

$\hat{f}(t_1,\ldots,t_{n-1})=g_1(\hat{s_1},\ldots,\hat{s_{n-1}})$

と表される(表されるまで $t_i$ の添字の番号が大きいものから消していって, (n-k)変数基本対称多項式を作れば良い).

そこで

$F(t_1,\ldots,t_n)=f(t_1,\ldots,t_n)-g_1(s_1,\ldots,s_{n-1})$

とする(右辺第二項が, $g_1(\hat{s})$ の場合と変わって「n変数」基本対称多項式になっていることに注意)と,

$s_i(t_1,\ldots,t_{n-1},0)=\hat{s}_i(t_1,\ldots,t_{n-1}), s_n(t_1,\ldots,t_{n-1},0)=0$

が一般に成立するから,

$\begin{array}{lcl} F(t_1,\ldots,t_{n-1},0) &=& f(t_1,\ldots,t_{n-1},0)-g_1(\hat{s_1},\ldots,\hat{s_{n-1}}) \\ &=& \hat{f}(t_1,\ldots,t_{n-1})-\hat{f}(t_1,\ldots,t_{n-1}) \\ &=& 0 \end{array}$

よってFは単項式として $t_n$ を因数に持つが, Fの対称性から $t_1t_2\cdots t_n=s_n$ を因数に持たざるを得ない. 結果として

$F(t_1,\ldots,t_n)=f-g(s_1,\ldots,s_{n-1})=s_nf_1(t_1,\ldots,t_n)$

を得て,

$f=g(s_1,\ldots,s_{n-1})+s_nf_1(t_1,\ldots,t_n)$

$f_1$ は総次数がnより低い対称式で, 有限回この操作を繰り返して問題のgを得る■

Proposition: 区間[a,b]上の単調増加関数f(x)の不連続点は高々可算個である
Proof: 区間[a,b]の或る点xにおいてf(x)が連続であるための必要十分は, xにおける振動量 $\displaystyle{ o(f,x)={\rm lim}_{\delta\rightarrow 0} \big\{ {\rm sup}_{|x-y|<\delta}f(y)-{\rm inf}_{|x-y|<\delta}f(y) \big\} }$ あるいは振幅 $\displaystyle{ a(f,x)={\rm lim}_{\delta\rightarrow 0}{\rm sup}_{y,z\in U(x,\delta)\cap [a,b]}|f(y)-f(z)|}$ が0に等しいことである. 振幅の記号を使って $A_n=\{x\in [a,b]|a(f,x)>1/n \}$ と定義すれば, fの不連続点全体の集合は

$A=\bigcup_{n=1}^\infty A_n$

と表せる. このAが零集合であることを示すことが目標であるが, 高々可算な零集合の可算和はまた零集合であって, Aの形からA_nが零集合であることを示せば良い.

[a,b]をN等分するような分割を⊿とおき, 分点 $a=a_0<a_1<\cdots < a_N=b$ によって作られるN個の区間 $\{I_j \}$ の振幅の総和はf(b)-f(a)以下である. すなわち

$\sum_{i=1}^N a(f,I_i)\leq f(b)-f(a)$

A_nは増加列A_1⊂A_2⊂…⊂A_n⊂…を持つので, 十分小さい任意の正数ε＞0についてA_ε={x∈[a,b] | a(f,x)≧ε}を被覆するものを考える. 区間列 $\{I_j \}$ でA_εと交わるものの開核を $I_j(1)^\circ,\ldots,I_j(k)^\circ$ とし, 漏れなく被覆するため分点{a_0,a_1,…,a_N}も付け加えて,

$A_\epsilon \subset I_{j(1)}^\circ \cup I_{j(2)}^\circ \cup \cdots \cup I_{j(k)}^\circ \cup \{a_0,a_1,\ldots,a_N\}$

となるようにする. 特に一点xに置ける不連続性はxの近傍における性質であるので, 必要なら分点Nを更に大きくとって各小開区間 $I_{j(*)}$ の幅を小さくし, 各々の区間 $I_{j(*)}$ に含まれる不連続点を唯一つにすることができる. {a_0,a_1,…,a_N}は長さの総和ε以下の開区間J_0,…,J_Nで覆う(J_j=(a_j-ε/2(N+1),a_j+ε/2(N+1))とすれば良い). 改めて書けば

$A_\epsilon\subset I_{j(1)}^\circ \cup I_{j(2)}^\circ \cup \cdots \cup I_{j(k)}^\circ \cup J_0\cup \cdots \cup J_N$

各 $I_{j(*)}^\circ$ 上 $a(f,I_{j(*)}^\circ)={\rm sup}_{x,y\in I_{j(*)}^\circ}|f(x)-f(y)| \geq a(f,x)\geq \epsilon \quad (x\in I_{j(*)}^\circ)$ であるから, k個の和を取って,

$f(b)-f(a)\geq ka(f,I_{j(*)}^\circ) \geq k\epsilon$

即ち $k\leq (f(b)-f(a))/\epsilon$ であるが, kは不連続点の個数であり, f(b)-f(a)が有限であるからkも有限である. 各 $I_{j(*)}$ は不連続点が唯一つ含まれるようにとってあるから, 不連続点はk個. J_*と同様にして長さの総和ε以下の開区間で被覆でき,

$|A_\epsilon|<2\epsilon$

である. Aはこのようなものの加算個で被覆されるから零集合である■

Proposition: 集合代数Mの「可算個の元A_1, A_2, …が互いに素ならその和集合はMに属す」はMがσ代数であることの十分条件である.

Proof: Mの任意の可算個の元A_1, A_2, …から互いに素なMの可算集合族A_k(1), A_k(2), …が構成できることを示せば良い.

可算集合族の可算和はまた可算和であるから, あるi∈NについてA_iが互いに素なMの可算集合族の和で表せれば良い.
A_iと異なる任意の可算集合族の元A_jとA_iとが互いに素ならそのような和としてA_i自身をとればよいから, A_iとある可算集合族の元が交わりを持つものと仮定する.
A_iと交わりを持つような族の添字集合をK_iとおくと, 仮定よりK_iの濃度に拠らず $\bigcup_{j\in K_i} A_j\in M$ であるから $(A_i-\bigcup_{j\in K_i} A_j) \in M$ .
直ちに $A_i = (A_i \cap \bigcup_{j\in K_i} A_j) \cup (A_i-\bigcup_{j\in K_i} A_j) \in M$ が互いに素なMの可算集合族の和の表現であると分かる■

Proposition: $G_{\delta\sigma}$ 集合, $F_{\sigma\delta}$ 集合はすべてボレル集合.
Proof: 位相空間 $(X,\mathfrak{O})$ を固定し, その $G_{\delta\sigma}$ 集合, $F_{\sigma\delta}$ 集合をそれぞれG, Fとする. 目標は $G\in \sigma(\mathfrak{O}), F\in \sigma(\mathfrak{O})$ を示すことである. Xのボレル集合族Bは, その完全加法性から, 開集合系と閉集合系の和, および各々の系に含まれる集合の可算和, 可算交叉, 可算差から生成されるもの全体であり, そうして生成されたBの元同士の可算和, 可算交叉, 可算差によっても閉じている. 従って $G_\delta$ は開集合の可算交叉で書けるものであるのでBに含まれ, また $G_{\delta\sigma}$ は $G_\delta$ の可算和であるのでまたBに含まれる. $F_{\sigma\delta}$ は $G_{\delta\sigma}$ の双対で, ド・モルガンの定理から $G_{\delta\sigma}$ の可算差に書けるから同様の議論でBに含まれる■

Proposition: 漸化式における「特性方程式」の意味を線型代数の立場から明確にせよ.
Proof: $a_{n+1}=ba_n+c$ を考える. 初項 $a_1=a$ とおいて, 数列のベクトル表記

$\begin{array}{lcl} \{a_n\} &=& (a,ab+c,ab^2+bc+c,\ldots), \\ \{a_{n+1}\} &=& (ab+c,ab^2+bc+c,ab^3+b^2c+bc+c, \ldots) \end{array}$

を得る. 初項aを決めれば数列の全ての要素が決まるので, $\ldots,ba_n+\mathbb{R},\ldots$ の形の数列全体をR加群として考えた空間Mにおける階数は1である( $\ldots,ba_n+c\ldots$ なる数列全体 $L$ はある要素の和 $b(a_n+a'_n)+2c$ を見れば分かるとおり, 加法について閉じていないので不十分). そこで包含写像 $\displaystyle{ \tau: a_n \mapsto \binom{a_n}{1}}$ によってaを直和空間 $M\oplus \mathbb{R}$ の元として考えたものを $\bar{a}$ とする. 即ち

$a \mapsto \bar{a}=\binom{a}{1} \in M\oplus \mathbb{R}$

そこでMにおける $\{a_n \}$ の各要素をτによって $M\oplus \mathbb{R}$ の元と捉えれば, 線型変換

$T:M\oplus \mathbb{R} \rightarrow M\oplus \mathbb{R}; T(\bar{a_n})=\bar{a_{n+1}}$

は, $\ldots,ba_n+c\ldots$ なる数列全体 $L$ と実数との直和 $L\oplus \mathbb{R} \subset M\oplus \mathbb{R}$ に始域を制限したとき, 終域も $L\oplus \mathbb{R}$ になる. つまり $L\oplus \mathbb{R}$ の中で作用が閉じている線形変換である.

Tは明らかに

$T= \begin{pmatrix} b & c\\ 0 & 1 \end{pmatrix}$

の形をしており, b≠0, b≠1を仮定するとき相異なる固有値b, 1が定まり, 対応する固有空間は

$\begin{array}{lclcl} W_b &=& {\rm Ker}\begin{pmatrix} 0&-c \\ 0&b-1 \end{pmatrix} &=& <(1,0)> \\ W_1 &=& {\rm Ker}\begin{pmatrix} 1-b&-c \end{pmatrix} &=& <(\frac{c}{1-b},1)> \end{array}$

この1に対する固有空間の生成系が特性方程式の解になっているが, 隣接3項間の漸化式に拡張した場合どうなるだろう.

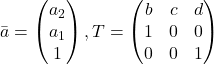$a_{n+2}=ba_{n+1}+ca_n+d$ に対して $\displaystyle{ \bar{a}=\begin{pmatrix} a_2 \\ a_1 \\ 1 \end{pmatrix}, T=\begin{pmatrix} b&c&d\\1&0&0\\0&0&1 \end{pmatrix}}$ とおいて同様の手続きで得られる固有空間を求めると,

$\begin{array}{lclcl} W_{\alpha_i} &=& {\rm Ker}\begin{pmatrix} 1&-\alpha_i&0 \\ 0&0&-d \\ 0&0& \alpha_i-1 \end{pmatrix} && \\ &=& \Bigg\{ \begin{array}{lcl} <(\alpha_i,1,0)> \quad (\alpha_i\neq 1, d\neq 0) \\ <(\alpha_i,1,0),(0,0,1)> \quad (\alpha_i\neq 1, d=0) \end{array} && \\\\ W_1 &=& {\rm Ker}\begin{pmatrix} 1-b&-c&-d \\ -1&1&0 \end{pmatrix} && \\ & = & \Bigg\{ \begin{array}{lcl} <(1,1,\frac{1-b-c}{d})> \quad (d\neq 0)\\ <(0,0,1)> \quad (b+c\neq 1, d=0) \\ <(1,1,0),(0,0,1)> \quad (b+c=1, d=0) \end{array} && \end{array}$

これらの形から, 隣接k項漸化式(k≧2)

$a_{n+k-1}=t_1a_{n+k-2}+t_2a_{n+k-3}\ldots+t_{k-1}a_n+t_k \quad (t_j\in \mathbb{R})$

を考えるとき, k=2の時とk＞2の時で特性方程式の意味が異なることが分かる.
k=2の時, 漸化式の定める係数拡大行列 $T$ の固有値1に対する固有空間を生成するベクトルの傾きである. k＞2においては $T$ の固有多項式から $\oplus \mathbb{R}$ 拡張した分の因数(x-1)を除いたものである■