昨晩は微妙な考察をしてたら夜が明けてしまいました(なぜ微妙かというと, 本筋からそれてしまったため)。
前半はそういう主旨です。
—————————————–
![]() を考える.
を考える.
2階までの導関数をとると,
![]()
![]()
よって![]() .
.
それにn階の導関数が![]() のn次多項式で表せることを踏まえて, 5階までの導関数を
のn次多項式で表せることを踏まえて, 5階までの導関数を![]() で表したとき, 係数行列
で表したとき, 係数行列![]() は次のようになります.
は次のようになります.
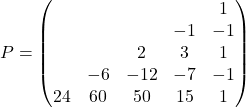
n階導関数におけるk次の項の係数を![]() と書くことにすれば, n階導関数は次のように書けることが分かります.
と書くことにすれば, n階導関数は次のように書けることが分かります.
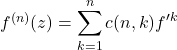
![]() は
は![]() 上正則で, 0において展開すると,
上正則で, 0において展開すると,
![]() となる.
となる.
一方![]() に対し,
に対し, ![]()
ここで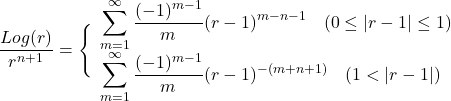
ちなみにこの係数関数![]() の要請は次の4つ.
の要請は次の4つ.
![]()
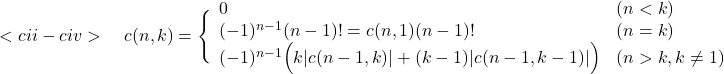
このような![]() を見つけることができれば, 恐らく
を見つけることができれば, 恐らく![]() の特異点
の特異点![]() 周りでの挙動をコーシーの積分表示式を用いずに見れる. これを見る限りガンマ関数に関係してそうですが..
周りでの挙動をコーシーの積分表示式を用いずに見れる. これを見る限りガンマ関数に関係してそうですが..
—————————————–
さて、話は変わって先日内法(うちのり)という言葉を知りました。
これは内側から測った底面積のことで、立方体上は単なる底面積のことらしい。
驚くべきことは、それが載っていたのは小学生の教材中だということ。