予定を管理するのは携帯ではまずいのですね。
電源が落ちそうなときに見れないとかなり面倒です。
12月に滋賀の高校に行くんですが、楽しみな一方、その準備に頭を痛めているのも事実。
普段高校生は見慣れているけれど、多様性を持っているとは言いがたい。土地柄か比較的「いい」親に生まれたのだろうなと思える子が来ているため、極端にまずい子はいない。
そんな子たちでも、僕にはどう付き合っていけばいいかが未だによく分からないことのほうが多い。
今日は買い物を行ったり洗濯でそれなりにやることはあったものの、ほぼ家で過ごしました。いやぁ、忘れてしまうものだなぁ・・・!
半年前にやったことなど、感覚レベルではもうすでに忘れかけている。
忘れないでおくために、こうして時々応用を追跡してみるのです。膨大だから限界はあるんでしょうが。
—————————————-
::multivariable taylor series theorem
z=(x,y)に対し, ![]() でz=(0,0)とするときのである.
でz=(0,0)とするときのである.
この場合, zとhを結ぶ線分が含まれるような, ![]() 上の任意の開円板上fが
上の任意の開円板上fが![]() classで,
classで,
![Rendered by QuickLaTeX.com \[f(h)=1+\sum_{m=1}^{k-1}\frac{(d^mf)_0(h)}{m!} + \frac{(d^kf)_{\theta h}(h)}{k!} \qquad (\exists \theta \in (0,1))\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-bc9449c83bf3c661b7e07c7884e03e8a_l3.png)
が成立してる.
但し![]() はm次形式で,
はm次形式で, ![]() (右辺の積は内積)及び
(右辺の積は内積)及び
![]() が成立している.
が成立している.
![]() なので,
なので,
![]()
つまり,
![Rendered by QuickLaTeX.com \[f(h)=1+\sum_{m=1}^{k-1}\frac{1}{m!}\sum_{l=0}^{m}\binom{m}{l}(ah_1)^{m-l}(bh_2)^l+\frac{e^{\theta(ah_1+bh_2)}}{k!} \sum_{l=0}^k \binom{k}{l}(ah_1)^{k-l}(by)^l\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-f9335c746c4b32ca4263acb455fd7394_l3.png)
そこでh=(1,1)のとき,
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} f(h) &=& e^{a+b} = \sum_{k=0}\frac{(a+b)^k}{k!} \\ &=& \sum_{k=0}\frac{1}{k!} \sum_{l=0}^k \binom{k}{l} a^{k-l}b^l \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-4c61debe2fdcd9b323c71d0caac0aaf6_l3.png)
の形になるが, これは上でmultivariableのtaylor seriesによって導かれた等式(にh=(1,1)を代入した時)と一致する. これらは理論上基本的なことだが, 手計算で改めて確認してみると新たな発見があることもある.
Proposition.1: ![]() 上の一変数有理関数体
上の一変数有理関数体![]() は代数閉体でない.
は代数閉体でない.
Proof.1: 背理法を使う. まず![]() が代数閉体であれば,
が代数閉体であれば, ![]() 上の多項式環
上の多項式環![]() の定数でない多項式が
の定数でない多項式が![]() 内に根を持つ. すなわち(
内に根を持つ. すなわち(![]() として),
として),
![]()
のようにfを定めるとき, f(r)=0となる![]() が存在する.
が存在する.
rがfの根であれば, rはまた![]() の根でもあるので, 初めから
の根でもあるので, 初めから![]() 上の一変数多項式環上での多項式の根としてrを捉えれば,
上の一変数多項式環上での多項式の根としてrを捉えれば,
![]()
を満たす有理関数![]() がある. しかしこのとき2次多項式の根の公式により,
がある. しかしこのとき2次多項式の根の公式により,
![]()
と表されるが, ![]() のときrは有理関数体の元という仮定に反する.
のときrは有理関数体の元という仮定に反する.
従って![]() は代数閉体である
は代数閉体である![]()
Proposition.2: 任意の有限群Gが与えられたとき, GをGalois GroupとするGalois extension field L/Kが存在する.
Proof.2: ![]() を適当な体F上のn変数有理関数体とし,
を適当な体F上のn変数有理関数体とし, ![]() のLへの左作用を
のLへの左作用を
![]()
と定義すれば, ![]() である.
である.
一方任意の有限群Gに対し, ある自然数![]() があってn次対称群
があってn次対称群![]() の部分群に同型なものが存在する. このnを固定して
の部分群に同型なものが存在する. このnを固定して![]() の部分群としてGを考えるとき, fixed field
の部分群としてGを考えるとき, fixed field ![]() に対し,
に対し, ![]() なので
なので![]() はGalois extensionである.
はGalois extensionである.
実際![]() とおいて,
とおいて, ![]() .
.
更に, Lのm+1個の元がK上線型従属となるので ![]() から結局
から結局![]() .
.
よって![]() はGalois extension
はGalois extension![]()
任意の与えられた有限(部分)群Gに対し, Gをガロア群とするガロア拡大体を対応させる写像![]() と, 有限次ガロア(中間)拡大体にそのガロア群を対応させる写像
と, 有限次ガロア(中間)拡大体にそのガロア群を対応させる写像![]() は互いに逆写像で, 次のような図式にカテゴリーの意味での可換性を持つことが知られている.
は互いに逆写像で, 次のような図式にカテゴリーの意味での可換性を持つことが知られている.
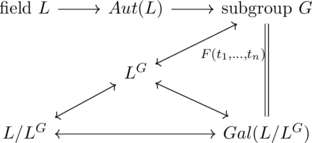
Proposition.3: Galois correspondence ![]() が与えられている. このとき次の3条件は同値である.
が与えられている. このとき次の3条件は同値である.
(GC6.1) M/KはGalois extension
(GC6.2) ![]()
(GC6.3) ![]()
Proof.3: (GC6.2)![]() (GC6.3):
(GC6.3): ![]() から
から![]() .
.
このとき![]() の元
の元![]() をとって
をとって
![Rendered by QuickLaTeX.com \[\begin{array}{lc} \forall \mu\in H, \sigma\mu\sigma^{-1}(y) = y & \Leftrightarrow \\ \forall \mu\in H, \mu\sigma^{-1}(y) = \sigma^{-1}(y) & \Leftrightarrow \\ \sigma^{-1}(y)\in L^H=M \quad \because {\rm Image}(\sigma)\subset L & \Leftrightarrow \\ y\in \sigma(M) & \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-b45e9356c9151f27f4899d28f1ba96c9_l3.png)
すなわち
![]() .
.
![]() の単射性から
の単射性から![]() により, (GC6.3)が従う
により, (GC6.3)が従う![]()
(GC6.1)![]() (GC6.2): 任意の
(GC6.2): 任意の![]() に対し,
に対し, ![]() .
.
M/KがGalois extensionであるから,
![]()
ガロア拡大の中間体とそのガロア群との対応の一意性により, ![]() .
.
つまり![]()
(GC6.2)![]() (GC6.1): 仮定から, 任意の
(GC6.1): 仮定から, 任意の![]() に対し
に対し![]() (Mを固定するため).
(Mを固定するため).
群準同型![]() を
を![]() と定義する
と定義する
(![]() から準同型になる).
から準同型になる).
このとき![]() であるから,
であるから, ![]() .
.
群準同型定理と![]() が部分群であることから,
が部分群であることから,
![]() .
.
改めて![]() を使うと,
を使うと, ![]() .
.
即ち![]() が成り立ち, M/KはGalois extensionということになる
が成り立ち, M/KはGalois extensionということになる![]()
ここで次のような考察を行った.
![]() となるような有限次ガロア拡大体の埋め込みを引き戻すことで, 行先の方程式をKummer extension内で級数的に解けないだろうか?
となるような有限次ガロア拡大体の埋め込みを引き戻すことで, 行先の方程式をKummer extension内で級数的に解けないだろうか?
これはつまり![]() の母関数として,
の母関数として, ![]() あるいは
あるいは![]() のようなものを求めることに等しい.
のようなものを求めることに等しい.
少なくとも完全体上の最小多項式は分離的なため, いわゆる通常のGalois体, すなわちMを含むK上最小のGalois拡大体を考えることで, 根が生成する体でそのような役割を果たすものがとれそうな気はする. しかしより平易な基による形式的冪級数表現を得ようとすれば, 可算無限拡大が出るように思えた.
実際に![]() をとって,
をとって, ![]() (但し
(但し![]() )を満たすようにK上の多項式関数列
)を満たすようにK上の多項式関数列![]() が取れたとする. このとき拡張多項定理より,
が取れたとする. このとき拡張多項定理より, ![]() に対し,
に対し,
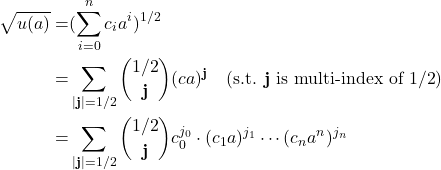
最後の項の分数次多項係数は, ガンマ関数による実数への拡張を通して次のように書ける(これは分数階数解析で矛盾無く定義されることが知られている).
![Rendered by QuickLaTeX.com \[\sum_{|\textbf{j}|=1/2} \frac{\sqrt{\pi}}{\Gamma(j_0+1)\cdots \Gamma(j_n+1)} c_0^{j_0}\cdot (c_1a)^{j_1} \cdots (c_na^n)^{j_n}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-3ca4cfd6d3bd7dbeae1ee158e70c89b7_l3.png)
ここで![]() は
は![]() を満たし, この範囲を連続的に動く.
を満たし, この範囲を連続的に動く.
複素数体上の超越数として知られる![]() が含まれるので,
が含まれるので, ![]()
これでは実数空間が得られてしまいそうだ. やはり形式冪級数和の演算について閉じた振る舞いをよく調べないといけない.
多様体Mから接ベクトルへの写像としてベクトル場![]() があたえられたとする. すなわち
があたえられたとする. すなわち![]() のようになる. このベクトル場
のようになる. このベクトル場![]() というのは, 多様体M上の各点pに, その点における流れの向きと速度を対応させたもの, という流体力学的意味づけが成されるが, ある軌道上の点pを時間tだけ流した位置を対応させる写像が群の性質を持つことから, ベクトル場と群とが対応する. このことをまとめると次のようになる.
というのは, 多様体M上の各点pに, その点における流れの向きと速度を対応させたもの, という流体力学的意味づけが成されるが, ある軌道上の点pを時間tだけ流した位置を対応させる写像が群の性質を持つことから, ベクトル場と群とが対応する. このことをまとめると次のようになる.
![]()
試しに楕円軌道を表すベクトル場として,
![]()
をとる(積分曲線![]() に関し, 定義より
に関し, 定義より![]() から, 微分方程式系
から, 微分方程式系![]() を解いたときに,
を解いたときに, ![]() となるように定めればよい.)
となるように定めればよい.)
上で出てきた2次行列をAとし, Aの特性x-行列を![]() とする. 特性方程式を解いて
とする. 特性方程式を解いて![]() .
.
![]() の適当な基本変形により,
の適当な基本変形により,
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} \bar{A}(x) &=& \begin{pmatrix}x&\alpha^{-1} \\ -\alpha & x \end{pmatrix} \\ & \sim & \begin{pmatrix} -\alpha & x \\ x & \alpha^{-1} \end{pmatrix} \\ & \sim & \begin{pmatrix} 1 & -x\alpha^{-1} \\ 0 & (x^2+1)\alpha^{-1} \end{pmatrix} \qquad (\alpha = \frac{b}{a}\neq 0) \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-e06513238f5e85cdad595cc6213e9e14_l3.png)
となるから, 固有値![]() に対応した固有空間
に対応した固有空間![]()
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} W_{\pm i} &=& {\rm Ker}[\bar{A}(\pm i)] \\ &=& {\rm Ker}[\begin{pmatrix}1&\pm i\alpha^{-1}\end{pmatrix}] \\ &=& <\pm i, \alpha> \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-b4fd3e6de055b70e67c2728a41902967_l3.png)
を得る. そこで![]() だから, 1 parameter group of transformations Gを
だから, 1 parameter group of transformations Gを![]() で構成する準備が整った.
で構成する準備が整った.
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} \exp{tA} &=& \sum_{n=0}\frac{t^n}{n!}A^n \\ &=& P\big (\sum_{n=0}\frac{t^n}{n!} \begin{pmatrix}i&0 \\ 0&-i\end{pmatrix}^n \big ) P^{-1} \\ &=& E\sum_{n=0}\frac{(-1)^nt^{2n}}{(2n)!} + A\sum_{n=0}\frac{(-1)^nt^{2n+1}}{(2n+1)!} \\ &=& \cos{t}\cdot E+\sin{t}\cdot A \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-d76f2bf0ef9518ea279425e5cc4a8844_l3.png)
この写像を改めて
![]()
と定義すれば, これがM上の任意の点pを時間t流した位置を対応付ける写像で, tの定義粋は実数全体に拡張でき, なるほど, 完備なベクトル場とはこのようなものか, と納得できる・・・・
と思ったのだが, 計算してみると, 一つ見落としがあったことに気づく…
![]() は
は![]() を満たさない!!
を満たさない!!
仕方が無いのでM上の任意の点pというのは諦めて, ![]() をとってやれば,
をとってやれば,
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} \phi_u(\phi_t(x=a\cos{s},y=b\sin{s})) &=& \begin{pmatrix} a(\cos{u}\cos(t+s)-\sin{u}\sin(t+s)) \\ b(\sin{u}\cos(t+s) + \cos{u}\sin(t+s)) \end{pmatrix} \\ &=& \begin{pmatrix} a\cos(u+t+s) \\ b\sin(u+t+s) \end{pmatrix} \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-33258b89a508df9579d74d23b393a8c6_l3.png)
が成り立つ(ちなみに原点を中心とした円を表すベクトル場![]() は, 同様の構成で任意点に対応して群を成した).
は, 同様の構成で任意点に対応して群を成した).
このことは, 原点を中心とし, pを通る円が(半径rによって)一意的に定まるのに対し, 原点を中心とし, pを通る楕円が無数に存在することに関係があることは恐らく確定だろう.
そこで原点を中心とし, pを通る楕円が一意的に定まるような空間を作って, その上で改めて群を構成すると良いと考えられる. そこで次の定義をする.
(非回転)楕円を規定する関数![]() を
を![]() と定義し, a, bが正数全体を動くとき, 原点を中心としpを通る(非回転)楕円上の点を
と定義し, a, bが正数全体を動くとき, 原点を中心としpを通る(非回転)楕円上の点を
![]()
とおくと, 商射
![]()
が定義される(実際に割られる空間が楕円の長辺と短辺を決定するタプル (a,b)全体![]() であり,
であり, ![]() がaとbに関する一次方程式であると同時に, pを通るという(x,y)に関する同値な条件に言い換えられている).
がaとbに関する一次方程式であると同時に, pを通るという(x,y)に関する同値な条件に言い換えられている).
実は, この同一視によって得られた空間は位相空間としてかなり扱いにくい.

![]() であることと
であることと![]() が自然な射影なので全射ではあるが,
が自然な射影なので全射ではあるが, ![]() 上の任意の2点が交わりを持つからHausdorffでない. また
上の任意の2点が交わりを持つからHausdorffでない. また![]() の任意点を含む
の任意点を含む![]() における開集合の被覆の重複度は無限次である. さらに, 任意の点
における開集合の被覆の重複度は無限次である. さらに, 任意の点![]() に関する性質
に関する性質![]() : xは, 点pを通る原点を中心とした(非回転)楕円上の一点であるは, 交わりについて閉じていない. つまり
: xは, 点pを通る原点を中心とした(非回転)楕円上の一点であるは, 交わりについて閉じていない. つまり![]() を満たす最小の部分集合, すなわち
を満たす最小の部分集合, すなわち![]() ,
, ![]() を満たす全ての
を満たす全ての![]() に対し,
に対し, ![]() なるMの部分集合Aは
なるMの部分集合Aは存在しない一点![]() のみである. 関係によって割られる空間は, 相異なる同値類の非交和で表現されるべきなので, 同値関係を得られない(具体的には推移律を満たさない⇒性質
のみである. 関係によって割られる空間は, 相異なる同値類の非交和で表現されるべきなので, 同値関係を得られない(具体的には推移律を満たさない⇒性質![]() を持つMの部分集合と持たない集合との直和に分割されない).
を持つMの部分集合と持たない集合との直和に分割されない).
———————————–
2013/11/26 訂正