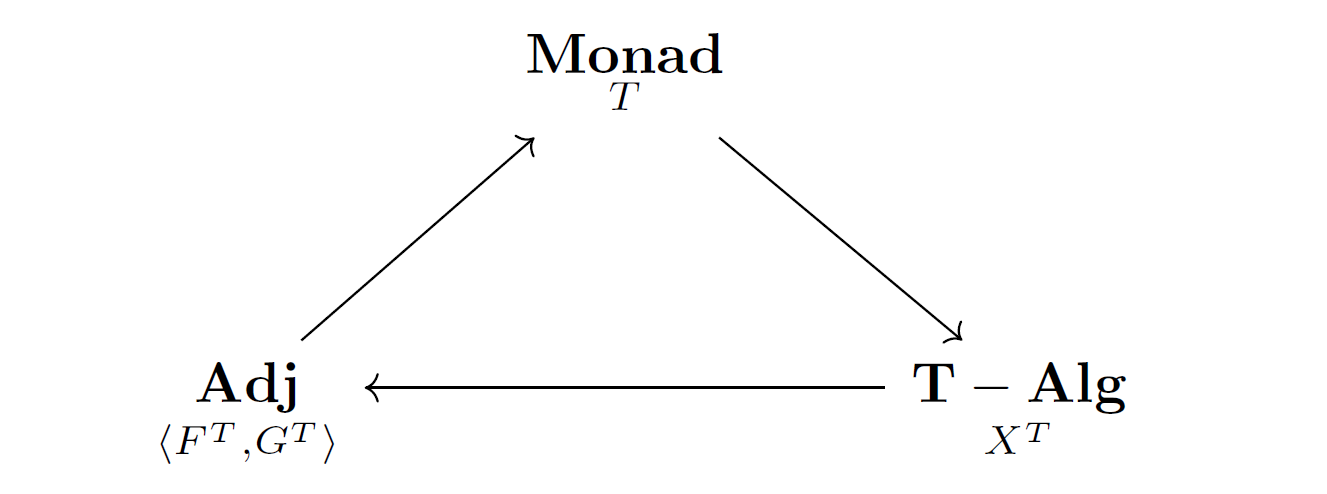
In this article, we will introduce a concrete example (found in CWM) of interchanging distinct structures of algebra and order on a fixed set, where a set of monoid action infers a special type of order called lattice in a guise of T-algebra.
Proposition. A partially ordered set Q is called complete semi-lattice when every subsethas supremum in Q. Let
be a covariant power set functor on Set. For a set
,
maps
to the set
and
maps each family of sets to the union set. a.
is a monad on Set; b. It holds that each
-algebra
is a complete semi-lattice if the order is defined by
and for each set
,
; c. Conversely, every small complete semi-lattice is
-algebra;
Proof of a. For the unit ![]() , we see that it commutes the diagram:
, we see that it commutes the diagram:

while for the product
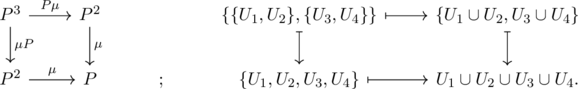
Note that every composition of the maps used in the left diagrams are horizontal compositions, where the functor ![]() is regarded as natural identity
is regarded as natural identity ![]() . On the right side of the diagram, we depicted an instance of element mapping considering
. On the right side of the diagram, we depicted an instance of element mapping considering ![]() as an element of powerset and as such.
as an element of powerset and as such.
□
Proof of b. First we show that ![]() is partially ordered.
is partially ordered.
The antisymmetry trivially holds. The reflexivity is by definition of ![]() -algebra
-algebra ![]() . The transitivity is also followed by definition. Assume
. The transitivity is also followed by definition. Assume ![]() and
and ![]() , then it is shown that
, then it is shown that ![]() as in the following commutative diagram:
as in the following commutative diagram:
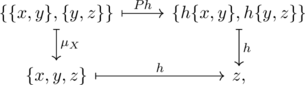
which concludes that
To see ![]() is a complete semi-lattice, we prove
is a complete semi-lattice, we prove ![]() indeed defines
indeed defines ![]() for each subset
for each subset ![]() . For any
. For any ![]() , we have
, we have ![]() and if there exists
and if there exists ![]() such that
such that ![]() , then
, then ![]() by definition; therefore
by definition; therefore ![]() .
.
□
Proof of c. Let ![]() be a complete semi-lattice. Then
be a complete semi-lattice. Then ![]() commutes the diagram:
commutes the diagram:

while
□