解析の話ですが、最近ベルヌーイ数を用いてベキ乗和の一般形を表示する証明を手がけました。
ベキ乗和の一般形とは, 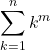 なる形で表される関数のことで、高校の範囲で公式化されているm≦3の場合を拡張し、全てのmについて(m,n)の関数表示をするのが目標です。
なる形で表される関数のことで、高校の範囲で公式化されているm≦3の場合を拡張し、全てのmについて(m,n)の関数表示をするのが目標です。
結論から言うと、不定形の極限として定まるベルヌーイ数(Bernoulli number)なる数によって漸近展開されます。自力でなんとかできたのは積分表示によるものでした。
17世紀初頭、ベルヌーイ、関孝和などの著名な数学者によってこの問題は証明されています。
———————————————————
![]() 次の数列の和の一般項を求めよう.
次の数列の和の一般項を求めよう.
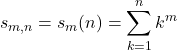
![]()
多項式関数列の有限和が有界でも, 自然数全体![]() の非稠密性から, 一般に項別微・積分が可能とは言えない. しかし有限ベキ和は 1. 極を持たず, 2. 単調増加であって, Taylor展開表示が可能であるという仮定は自然である. 従って項別微・積分可能性も肯定できるのである.
の非稠密性から, 一般に項別微・積分が可能とは言えない. しかし有限ベキ和は 1. 極を持たず, 2. 単調増加であって, Taylor展開表示が可能であるという仮定は自然である. 従って項別微・積分可能性も肯定できるのである.
そこで次の関係式を得る.
![]()
また明らかに,
![]()
これらは初期値を与える.
一方
![]()
とおけば,
![]()
であって
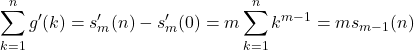
そして第2, 第4項を逐次微分していくと,
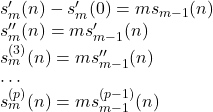
のようになる.
そこで![]() とおき, 各段階において
とおき, 各段階において![]() を代入していくと,
を代入していくと,
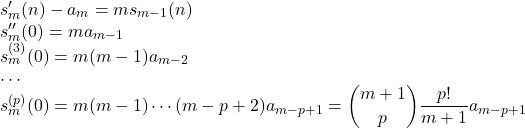
![]() を
を![]() 周りでm+1項までTaylor展開して
周りでm+1項までTaylor展開して
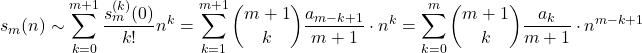
今 n=1 とおいて第1項と第4項をまとめると,
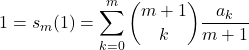
実はこの![]() はBernoulli数
はBernoulli数![]() の定義
の定義
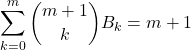
を満たす.
すなわち![]() (一意性, 一様収束性については後で議論します).
(一意性, 一様収束性については後で議論します).
よって上式を変形し, ベキ乗和の公式の一般形が得られた.
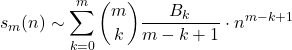
———————————————————
次にBernoulli数の性質を, 上のベキ級数を無限次元多項式環とみて代数的・組み合わせ論的考察をしてみよう.
そのためにまず次の補題を示す.
(Lemma-i) m, n∈Z; (m)+(n)=(d), (m)∩(n)=(l) ⇒ d,lはそれぞれm,nの最大公約数, 最小公倍数である.
mは(m)に含まれる正整数のうち最小でなくてはならない.
実際mが最小でなければ, ![]() となるrが存在してしまい, m-r≠Zmであって矛盾である. これは(n)についても同様のことが言える.
となるrが存在してしまい, m-r≠Zmであって矛盾である. これは(n)についても同様のことが言える.
そこでm,nが互いに素なら, (m)+(n)=(1)で, d=1.
逆に公約数dを持てば(m)+(n)=(d) (d≠1).
前者では最大公約数=最小公約数であってこのままで良い.
後者で![]() なる公約数eがあれば, eはdの約数で(m)+(n)=(e)が成立しなくてはいけない.
なる公約数eがあれば, eはdの約数で(m)+(n)=(e)が成立しなくてはいけない.
ところが(m)+(n)=(d)でもあるからRm+Rn=1d not in (e). これは矛盾であるからdはm,nの最大公約数.
また(m)∩(n)∋x=Rmnであるから(l)=(mn)となるのは明らか. lの最小性は上記に挙げた単項イデアル環の最小性によって示される.