H space (spanier) – 解析タネル

Introducing H space along with the Spanier’s text Algebraic Topology.
The proof in the article is basically same in the book, except that I put somewhat more detail.

covariant functor $\pi_X$
For any given category C, and object $X\in C$ , we always have a covariant functor $\pi_X:C\to {\bf Set}$ defined by $\pi_X(Y)=hom(X,Y)$ for an object of set. And for any morphism of C, let $f\in hom(Y,Z)$ for any $Y,Z\in Ob(C)$ , then the morphism function is defined by $f_*(\lambda)=f\circ \lambda$ for any element $\lambda\in hom(X,Y)$ ( $f_*=\pi_X(f):\pi_X(Y)\to \pi_X(Z)$ ).

We can check the identity law: $\pi_x(id_Y)(\lambda)=(id_Y)_*(\lambda)=\lambda, \forall \lambda\in \pi_X(Y)$ , and the composite law:

Rendered by QuickLaTeX.com

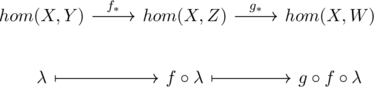
initial object

For given category C, X the object of C, is called initial object if for any object Y, $hom(X,Y)$ consists of only one element of morphism in C. We can characterize the initial object of a category C with the functor $\pi_X$ as:

$X:\ initial\ object\ of\ C\Leftrightarrow\ {\rm Im}\pi_X \text{is equivalent to a discrete subcategory of}\ {\bf Set}.$

Discrete subcategory of ${\bf Set}$ is always regarded as a family of sets (because the morphisms are only the identity of those objects). Thus the equivalence between category in this sense does not indicate they are same; rather, this is because we can instantly observe that there is 1 to 1 correspondence $\pi_X(Y)\leftrightarrow Y$ if X is initial object in C.

construction of the category of directed system

$\Lambda$ is directed set. $\{Y^\alpha,f_\alpha^\beta\}_\Lambda$ is directed system (i.e. the sequence of morphisms and objects which satisfy the following conditions).

(1) $f_\alpha^\alpha=id_{Y^\alpha}$
(2) $f_\alpha^\gamma=f_\beta^\gamma f_\alpha^\beta$ for all $\alpha\leq \beta\leq \gamma$

The object of the category is again a sequence of morphisms $\{g_\alpha : Y^\alpha \to Z\}_\lambda \in Ob(C)$ s.t.
the diagram

Rendered by QuickLaTeX.com

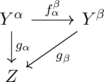
commutes. Note that the range Z is fixed. And for morphism of the category, $h\in hom(\{g_\alpha : Y^\alpha \to Z\}_\lambda,\{g'_\alpha : Y^\alpha \to Z'\}_\lambda)$ is a map $h:Z\to Z'$ s.t.

Rendered by QuickLaTeX.com

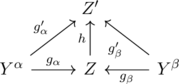
commutes. The initial object of the category C, called direct limit of the direct system $\{Y^\alpha,f_\alpha^\beta\}_\Lambda$ . We can construct the category of $inv\{Y^\alpha,f_\alpha^\beta\}_\Lambda$ and the inverse limit of the inverse system, in a similar manner.

category of pointed topological space

We denote ${\bf hTop^*}$ as the homotopy category of pointed topological space. The objects are pointed spaces denoted by $(X,x_0)$ (the base point is determined uniquely for each topological space). The morphisms are homotopy classes of base point preserving continuous maps between pointed topological spaces. Shortly we denote $[X;P]$ in place of $hom((X,x_0),(P,p_0))$ (the composition law for the morphisms is confirmed based on the known fact that

“the composition of homotopic maps rel $A,\ B$ are homotopic rel $A$ if $f_1(A)\subset B$ ( $f_1,f_2:(X,A)\to (Y,B)$ are homotopic maps)”.

Thus the composition can uniquely determined independent to the choice of the representation from the homotopy class).

When a topological group $P$ is given, $\pi^P$ defines a contravariant functor

$\pi^P : {\bf hTop}^*\to {\bf Grp}$

Admitting the above fact without proof(c.f. Spanier pp.34), we rather want to obtain a functor without assuming that P is a group.

To do this, we shall assume that P is a pointed space, and consider the situation where $[X;P]$ has group structure but not the set of basepoint-preserving continuous maps from X to P.

Let P’ is a topological group, $F:P\to P'$ is an equivalence in ${\bf hTop}^*$ (we don’t assume P is a group), and $f\in [X;Y]$ . Then the diagram

Rendered by QuickLaTeX.com

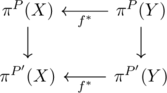
commutes and the vertical arrows are isomorphisms (in the category of group induced from topological group P’ by pointwise multiplication) and thus $\pi^P$ and $\pi^{P'}$ are naturally equivalent and the output of the group structure are unchanged when $P\sim P'$ in homotopy. $[X;P]$ becomes group with

$\lambda_1\lambda_2(x)=(F\circ\lambda_1)(x)(F\circ\lambda_2)(x),\ (F:P\simeq P',\ \lambda_1,\lambda_2\in [X;P])$

condition of a functor $\pi^P$ to have a range in ${\bf Grp}$

We have this result.

Theorem 5.

P: pointed space. Then P is an H group iff $\pi^P$ is a contravariant functor

$\pi^P:{\bf hTop}^*\to {\bf Grp}$

First we define some terminologies.

H space is a pointed topological space P together with a continuous multiplication

$\mu:P\times P\to P$

for which the (unique) constant map $c:P\to P$ is a homotopy identity (i.e. the composition maps

$P\overset{(c,1)}{\to} P\times P \overset{\mu}{\to} P,\ P\overset{(1,c)}{\to} P\times P \overset{\mu}{\to} P$

are homotopic to $1_P$ .

homomorphism of H spaces P, P’ with multiplications $\mu$ and $\mu'$ is a continuous map $\alpha:P\to P'$ s.t. following diagram :

Rendered by QuickLaTeX.com

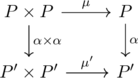
is homotopy commutative. This definition may sound instinctive when we regard the homomorphism of H spaces as continuous map compatible with the continuous multiplication of H spaces in ${\bf hTop^*}$ .

We will prove the following theorem, and then the theorem 5 follows immediately.

For the reason that the techniques used in the proof seems somewhat common when it comes to put an algebraic-like structure to a topological object, which repeatedly appears in the further discussion, we give a detailed proof.

Theorem 4.

A pointed space having the same homotopy type as an H space (or an H group) is itself an H space (or H group) in such a way that the homotopy equivalence is a homomorphism.

pf. Let $f:P\to P'$ and $g:P'\to P$ be homotopy inverses and let $P$ be an H space with multiplication $\mu:P\times P\to P$ . Define $\mu':P'\times P'\to P'$ to be the composite

$P'\times P'\overset{g\times g}{\to} P\times P\overset{\mu}{\to} P \overset{f}{\to} P'$

$\mu'$ is a continuous multiplication in $P'$ and the composite

$P'\overset{(1,c')}{\to} P'\times P' \overset{\mu'}{\to}P'$

equals the composite

$P'\overset{g}{\to} P \overset{(1,c)}{\to} P\times P \overset{\mu}{\to} P\overset{f}{\to} P'$

, which is homotopic to the composite $P'\overset{g}{\to} P \overset{f}{\to} P'$ . Because $fg\simeq 1_{P'}$ , the map $\mu'\circ (1,c')$ is homotopic to $1_{P'}$ . Similarly, the map $\mu'\circ (c',1)$ is homotopic to $1_{P'}$ . Therefore P’ is an H space (we checked $c'$ is the homotopy identity right now). Because the square

Rendered by QuickLaTeX.com

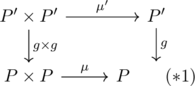
is homotopy commutative (just compose $f\times f$ from the right of $\mu'$ ), $g$ is a homomorphism (by definition), and so is $f$ (since $\mu'\circ (f\times f)=f\circ\mu\circ (g\times g\circ f\times f) \sim f\circ \mu$ , the vertical arrow can be reversed). If $\mu$ is homotopy associative or homotopy abelian, so is $\mu'$ , and if $\phi:P\to P$ is a homotopy inverse for P, then $f\phi g:P'\to P'$ is a homotopy inverse for P’.

We prove the last statement.

1. $\mu'$ is associative (when $\mu$ is)

Consider the following diagram.

Rendered by QuickLaTeX.com

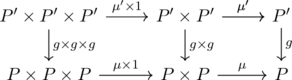
Then we can obtain

$\mu'\circ (\mu'\times 1)\sim f\circ (\mu\circ (1\times \mu))\circ g^3 \sim \mu' \circ (1\times \mu')$

from the diagram (*1). The last homotopy equivalence can be attained with another diagram replacing $\mu\times 1$ with $1\times \mu$ , respectively.

2. $\mu'$ is homotopy abelian (when $\mu$ is)

In the similar manner above, consider the following diagram.

Rendered by QuickLaTeX.com

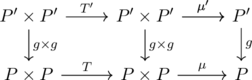
The composition of the bottom arrows, $\mu\circ T$ is homotopic to $\mu$ . So we get

$\mu'\circ T\sim f\circ \mu\circ (g\times g)=\mu'$

3. $f\phi g:P'\to P'$ is a homotopy inverse for P’ (if $\phi:P\to P$ is for P)

Again, consider the following diagram.

Rendered by QuickLaTeX.com

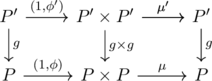
I’m actually unclear about the existence of $\phi'$ (I mean, as a non-trivial map naturally induced by the given homotopy inverse $\phi$ ), but if it exists, then it must commutes on the left side of diagram and it must agree with $f\phi g$ .

Given an H space P, for any pointed space X there is a law of composition in $[X;P]$ defined by

$[g_1][g_2]=[\mu\circ (g_1,g_2)]$

The resultant of the multiplication is a homotopy class of continuous map

$x\mapsto g_1(x)g_2(x)$

and this is well-defined (again $[X;P]$ is a set of morphisms in ${\bf hTop}^*$ !)

If P is a H group, then for $[g]\in [X;P]$ , the inverse is $[\phi\circ g]$ . Since $g(x)\in P$ for any $x\in X$ ,
$[g][\phi\circ g]=[\mu\circ (g,\phi\circ g)]=c$ .

Therefore, we have the theorem 5 (partially, but not discussing here although reverse is also true).