common cellular structures on a topological space and their properties

Despite the cellular structure on a space is a fundamental ingredients of algebraic topology, this topic seems likely to cause people a subtle confusion and unfortunately, they have not been simple to summarize the distinct properties of each structure with a good references.

Here I list and explain seven important properties that bound to characterize each structures.

		simplicial	delta	singular-delta	CW	Cell
1	distinct faces of a simplex can be glued together	x	o	o	o	o
2	a simplex can intersect transversally with another simplex in which the intersection is not composed of the union of cells	x	x	x	x	x
3	for all n>=1, a (n-1)-simplex must correspond to each face of a n-simplex	o	o	x	x	x
4	for all n>=1, a (n-1)-simplex must uniquely correspond to each face of a n-simplex	o	x	x	x	x
5	for all n>=1 and some λ<=(n-1), a λ-simplex must correspond to each face of a n-simplex	o	o	o	x	x
6	admits weak/initial topology by the family of characteristic maps	o	o	o	o	x
7	admits closure finiteness property for each cell	o	o	o	o	x

1. distinct faces of a simplex can be glued together

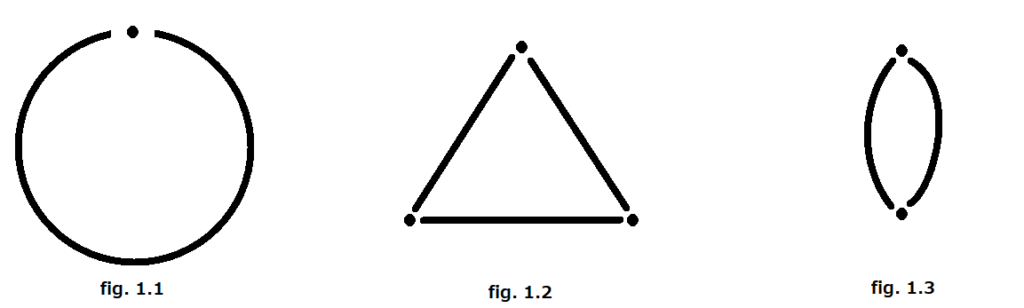
The figure 1.1 explains how gluing in a simplex is not permitted in the simplicial structure. More precisely by the abstract simplicial notion, a set of vertices uniquely determine a simplicial simplex; therefore the figure 1.3 does not admit simplicial structure (two vertices cannot distinguish a 1-simplex). Figure 1.2 is the minimal simplicial decomposition of $S^1$ , a circle.

2. a simplex can intersect transversally with another simplex in which the intersection is not composed of the union of cells

This cannot occur in any cellular structures on a space since the structure requires decomposition of the space into disjoint union of cells in the level of cell complex; all other cellular complexes are cell complex by definition (cell is the interior image of a standard simplex by a characteristic map).

3. for all 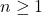$n\geq 1$ , a (n-1)-simplex must correspond to each face of a n-simplex

This denotes the major difference of delta complex from CW complex – for delta complex, the restriction of a characteristic map to each face of n-simplex is the distinguished characteristic map for some (n-1) cell, yet the restriction is not necessarily a characteristic map for CW complex, moreover the boundary image of n-simplex in CW complex has only limited to be contained in the union of a finite number of cells of dimension less than n.

4. for all 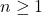$n\geq 1$ , a (n-1)-simplex must uniquely correspond to each face of a n-simplex

As explained earlier in the property 1 section, the uniqueness property can be restated that a set of vertices determine the unique simplicial simplex.

5. for all 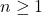$n\geq 1$ and some 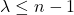$\lambda\leq n-1$ , a $\lambda$ -simplex must correspond to each face of a n-simplex

As defined in [Hatcher, p.535], the singular delta complex is more general version of a delta complex to allow cells to be attached by arbitrary simplicial maps. The property attributes the extensive degree of a cell that is allowed to be collapsed in the image of a characteristic map.

6. admits weak/initial topology by the family of characteristic maps

This property actually is a part of the definition of CW complex. The following example explains why a cell complex may not offer the topology.

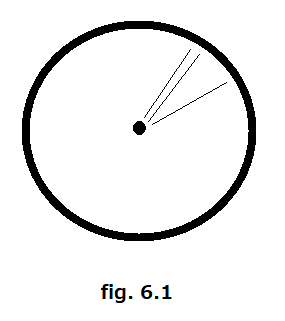
In the figure 6.1, the image pictures a decomposition of a disk: the boundary is composed of a collection of singletons as 0-cells, the radius is all filled with 1-cells and the center is another 0-cell.
For the disk $X$ , consider a subspace in spherical coordinate $A\subset X$ written as:

$A=X\backslash (0,r]\times \{0\},$

where r is the radius. $A$ is neither closed nor open in the subspace topology of $\mathbb{R}^2$ , which in turn becomes incompatible with the weak topology; the inverse image of a characteristic map intersects with the standard simplex both in closed and open set, concluded that $A$ is a clopen set in weak topology.

7. admits closure finiteness property for each cell

As in the previous one, this property also is a part of the definition of CW complex. Again the following figure is a decomposition of a disk into a collection of 0-cells in its boundary and a 2-cell in the interior attached in obvious manner.

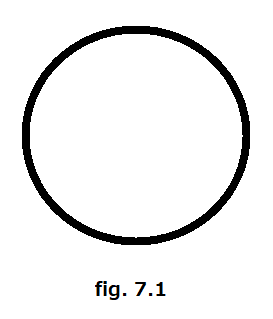
The closure of 2-cell coincide with the disk itself and therefore intersects with infinitely many 0-cells in the boundary.

References

[Hatcher] Allen Hatcher, Algebraic Topology, 2002.