A general method of constructing a colimit

While a colimit is of a typical object in category theory hence so much in the closely related areas such as categorical logic and type theory, its construction can be a nuisance especially within a strict category setting where elementhood matters in the objects.

We describe a concrete method of “generating an element of colimit” in terms of so called solution set as a part of necessary and sufficient conditions of adjoint functor theorem.

While the idea is not original and the contents are parallel to the CWM^[1]MacLane, S. (1971). Categories for the Working Mathematician. New York: Springer-Verlag., we believe that the exposition is helpful and unique in the applicable interpretation.

1. The solution set condition and its interpretations

The solution set condition, originally formalized as a necessary condition that a functor (under some condition) becomes right adjoint, is an interesting assertion by itself simply because it gives an explicit construction of a colimit.

More precisely, solution set condition denotes the existence of “weakly universal objects” in some sense that can be expressed (or unified) in terms of functor involved with the following (general) adjoint functor theorem and its corollaries:

Adjoint functor theorem;
Condition for the existence of initial object;
Representable functor theorem.

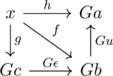
Although we are not giving any proofs and unnecessary only for the exposition, we denote by $A$ a locally small, complete small category. We also fix a functor $F:A\to X$ where the selection of a category $X$ is the key to characterize what the solution set is for. We persist in these notations throughout the part 1.

With these in mind, the (unified) solution set condition is concisely stated as:

$\forall x\in Ob(X),{\rm wInit}(x\downarrow F)\neq \emptyset. \quad … \quad (*S)$

Here wInit denotes a (small) set of weakly initial objects, whose element suffices the condition of initial object except the uniqueness condition. (*S) can be stated explicitly as:

$(\forall x\in Ob(X))(\forall a\in A)(\forall h:x\to Fa)(\exists a'\in A)(\exists f:x\to Fa')(\exists t:a'\to a)(h=Ft\circ f). \quad … \quad (*S')$

While (*S) is exactly the solution set condition for adjoint functor theorem, the condition will be interpreted accordingly in a context.

1.1. Condition for the existence of initial object

By setting $X={\bf 1}$ , dropping $\forall x\in Ob(X)$ and letting $F:A\to{\bf 1}$ the constant functor, we obtain a necessary condition for the existence of initial object, namely:

${\rm wInit}(1\downarrow F)\neq \emptyset.$

Notice that $F$ canonically preserves every (small) limits because any universal cone $\tau:a\xrightarrow{\cdot} P\in A^J$ collapses to the zero object in ${\bf 1}$ .

1.2. Representable functor theorem

This is analogous to the condition for the existence of initial object.

For $X={\bf Set}$ , a representation of $F:A\to X$ is identified with the universal arrow ${\rm Init}(* \downarrow F)$ , or equivalently the unit of adjoint $\eta:I_{\bf 1}\xrightarrow{\cdot} F'S$ , where ${\bf 1}$ is identified with the faithful subcategory $\{*\}\subset X={\bf Set}$ and $F'$ the composition of $F$ followed by $X\to {\bf 1}$ , furthermore $S:{\bf 1}\to A$ a choice functor.

Therefore $F$ is representable if and only if ${\rm wInit}(* \downarrow F)\neq \emptyset$ and $F$ preserves small limit.

2. Subobjects and spanning maps

For an arbitrary category $A$ , we can consider “subobjects” of an object $a\in A$ , whose elements are monos $u:b\to a$ together with the order relation defined by $u\leq v$ if and only if there exists some $u':b\to b'$ and a mono $v:b'\to a$ such that $u=v\circ u'$ , or to say concisely $u$ factors through $v$ . By defining $(u\leq v) \wedge (v\leq u) \iff u=v$ , we call the set of equivalence classes subobjects of a. We denote subobjects of a by $Sub(a)\in {\bf Pos}$ .

Definition 2.1. For a given functor $G:A\to X$ , a map $f:x\to Ga$ is said to span a when there is no (non-isomorphic) mono $s\to a$ such that $f$ factors through $Gs\to Ga$ .

Lemma 2.2. Fix a category $A$ and its object $a\in A$ .
Suppose the pullbacks for any set of subobjects $S\subset Sub(a)$ exists, namely $\cap S\in Sub(a)$ . If a functor $G:A\to X$ preserves any of such pullbacks, then every map $h:x\to Ga$ factors through a map $f:x\to Gb$ that spans $b$ .

Proof of lemma 2.2. For $h:x\to Ga$ , let $U={u_i:b_i\to a}\subset Sub(a)$ be a set of subobjects such that $\exists f_i:x\to Gb_i$ with $h=Gu_i\circ f_i$ for each i. Since by assumption there exist the pullback $\cap U\in Sub(a)$ which we denote as $u:b\to a$ , we see it suffices $h=Gu\circ f$ , where $f$ is the induced map on pullback diagrams of $\{Gb_i\xrightarrow{Gu_i} Ga \xleftarrow{Gu} Gb\}_i$ .

$f$ apparently spans $b$ by the construction of $U$ ; precisely, if there is a mono $(\epsilon:c\to b)\in Sub(b)$ such that $f$ factors through $G\epsilon$ for some $g:x\to Gc$ (i.e. $f=G\epsilon\circ g$ ), then $u\circ\epsilon\in Sub(a)$ must be in $U$ and since $u$ is the pullback, $c$ must coincide with $b$ , analogously $g$ with $f$ and $\epsilon$ with $id_b$ .

Rendered by QuickLaTeX.com

□

3. A general method of constructing a colimit as the result of a left adjoint functor from Set

It is an immediate consequence of adjoint functor theorem that we have a general method to construct a colimit of certain type in a particular class of categories.

The applicable class of categories represented by $C$ should suffice the following properties (*AFT):

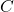$C$ is locally small and complete small;
It is given a continuous functor 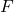$F$ to ${\bf Set}$ ;
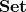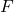$F$ suffices solution set condition (*S).

Not exclusive yet particularly important instance of such classes is the algebraic system of fixed type, which forms a category of algebra ${\bf Alg}_\tau$ of given type $\tau$ . ${\bf Alg}_\tau$ suffices (*AFT) along with the functor known as forgetful functor $U:{\bf Alg}_\tau\to {\bf Set}$ .

If we are given such functor with these properties, adjoint functor theorem states that the continuous functor $F:C\to {\bf Set}$ admits a left adjoint, which preserves a colimit of ${\bf Set}$ , hence the image of the left adjoint is the constructed colimit in $C$ .

Moreover, this construction procedure can be done in an algorithmic manner. Above lemma shows that, the solution set ${\rm wInit(x\downarrow F)}$ of $x\in C$ can be identified with the union set of maps that span from $x$ . This can be seen as follows:

To a given map , choosing a map  through which  factors is equivalent to inducing a (part of) pullback map  in the diagrams of the form .

This last description roughly speaks of algorithmic nature of a (co)limit preserving condition of procedure (i.e. functor), namely providing with a “basis” in the target category against an arbitrary object of source category.
Here we mean by “basis” is a set of objects that admit irreducibleness of some sort (c.f. might be preferable to express as “atomicity” in a context).

Here is an example.

3.1. Coproduct in Grp

In ${\bf Grp}$ , the forgetful functor $U:{\bf Grp}\to{\bf Set}$ admits the free group construction $F$ as the left adjoint, where a solution set of $s\in {\bf Set}$ is composed of every monomorphisms of the form $s\to Ut$ that has no factoring monos $s\to Ut'$ through a subgroup $t'\to t$ . Hence $s$ plays a part of freely generating (as a group) set for $t$ .

The free construction preserves colimit (direct sum) $A\sqcup B$ of ${\bf Set}$ , hence the coproduct is justified to have the form $F(A\sqcup B)$ in ${\bf Grp}$ , meaning that an element of $F(A\sqcup B)$ is obtained by (finite applications of) group operations and identities on the base set $A\sqcup B$ in terms of universal algebra.

Footnotes[+]

Footnotes
↑1	MacLane, S. (1971). Categories for the Working Mathematician. New York: Springer-Verlag.