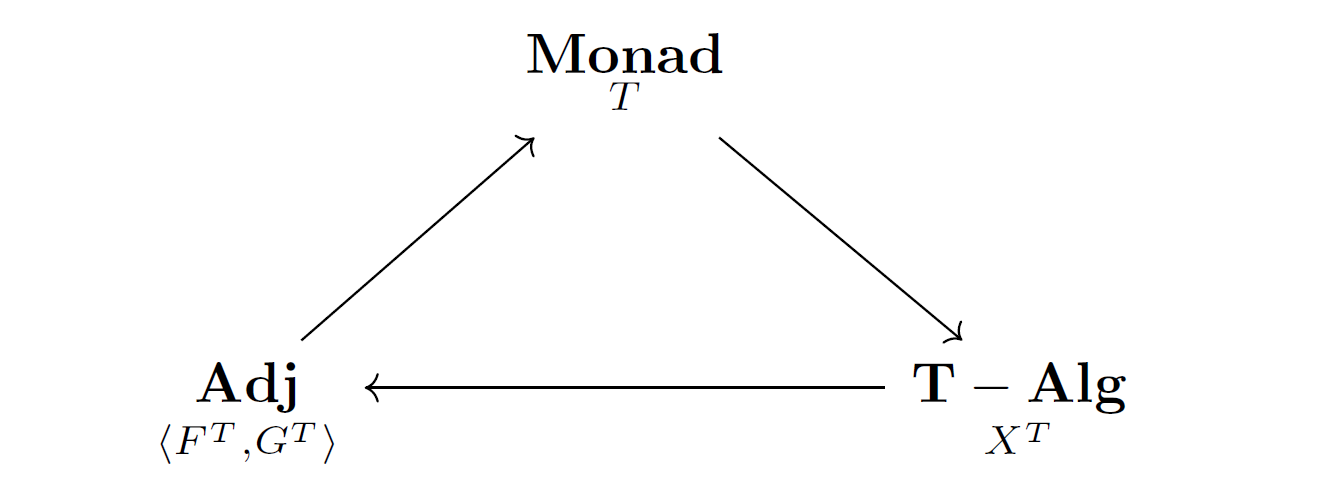
A small example of algebra turns out to be a semi-lattice

In this article, we will introduce a concrete example (found in CWM) of interchanging distinct structures of algebra and order on a fixed set, where a set of monoid action infers a special type of order called lattice in a guise of T-algebra.

Proposition. A partially ordered set Q is called complete semi-lattice when every subset has supremum in Q.

Let be a covariant power set functor on Set. For a set , maps to the set and maps each family of sets to the union set.

a. is a monad on Set;
b. It holds that each -algebra is a complete semi-lattice if the order is defined by and for each set , ;
c. Conversely, every small complete semi-lattice is -algebra;

Proof of a. For the unit $\eta$ , we see that it commutes the diagram:

while for the product $\mu$ , we see that it commutes the following diagram:

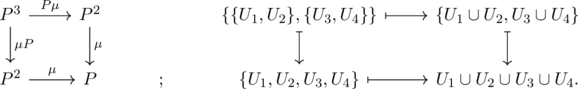
Note that every composition of the maps used in the left diagrams are horizontal compositions, where the functor $P:{\bf Set}\to {\bf Set}$ is regarded as natural identity $P:P\xrightarrow{\cdot} P$ . On the right side of the diagram, we depicted an instance of element mapping considering $U_i\in PX$ as an element of powerset and as such.

□

Proof of b. First we show that $X$ is partially ordered.

The antisymmetry trivially holds. The reflexivity is by definition of $\mathcal{P}$ -algebra $id_X=h\circ \eta_X$ . The transitivity is also followed by definition. Assume $x\leq y$ and $y\leq z$ , then it is shown that $x\leq z$ as in the following commutative diagram:

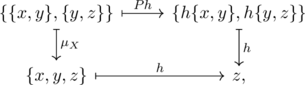
which concludes that $X$ is partially ordered.

To see $X$ is a complete semi-lattice, we prove $h$ indeed defines $\sup$ for each subset $S\subset X$ . For any $z\in S$ , we have $h\{z,hS\}=(h\circ \mu_X) \{\{z\},S\} = h(\{z\}\cup S)=hS$ and if there exists $z\in X$ such that $h\{z,hS\}=z$ , then $hS\leq z$ by definition; therefore $hS=\sup S$ .