パップス・ギョルダンの定理です.
回転体の体積を高速で求める必要があり, 色々調べてみるとかなり使い勝手が良かったので紹介.
定理. 回転軸Aを固定し, Aと交わらない任意に与えられた二次曲線を![]() とする(一般の,
とする(一般の, ![]() 級のもので, 二次曲線の端点とAは接触しても良い). このとき, Aを中心に回転させた回転体の体積Vは, Cの面積S, 重心とAとの距離Lに対し,
級のもので, 二次曲線の端点とAは接触しても良い). このとき, Aを中心に回転させた回転体の体積Vは, Cの面積S, 重心とAとの距離Lに対し,
![]()
を満たす.
※座標系が直交でない場合は基底を正規化すれば常に直交座標を取れるので, 以下では直交座標で議論します((u, v)座標系で表される二次曲線![]() の直交座標系における関数は, 座標変換を与える同相写像
の直交座標系における関数は, 座標変換を与える同相写像![]() に対し,
に対し, ![]() です).
です).
以下比較のため通常の回転体の体積の求め方です.
上で注意した座標変換, 平行移動, 鏡映を合成して, 曲線を定義する関数sに繰り込んでしまえば, x軸を回転軸とし, sのグラフが常に上半平面にあるようにすることができる. C上ヤコビアン![]() を満たす任意の点(とその近傍)で
を満たす任意の点(とその近傍)で![]() となるものが存在する. 特にpの付近で多価となるものはこのようなyは一意的には定まらないが, 直線
となるものが存在する. 特にpの付近で多価となるものはこのようなyは一意的には定まらないが, 直線![]() から曲線Cが切り取る長さの総和をすべてのxについて
から曲線Cが切り取る長さの総和をすべてのxについて![]() と定義すれば, これは回転させる時の半径を与える. ∴
と定義すれば, これは回転させる時の半径を与える. ∴![]()
この体積の求め方は分かりやすいですが, 計算量においてパップス・ギョルダンの方法に劣ることがある場合は次のような時です.
- 多価である場合: 場合分けし, 各々の切り取る切片の総和
- 左右対象である場合: 計算量がどちらも半分になる
ギョルダンの方法では, まずCの重心座標を求める必要があります. 上と同様Cの面積をSとすれば, 重心の座標![]() は次で与えられます.
は次で与えられます.
![]()
ここで![]() は, それぞれx方向, y方向に積分する時の微小面積要素で,
は, それぞれx方向, y方向に積分する時の微小面積要素で, ![]() は
は
「xを固定した時のグラフの(n-1)次元体積, つまりyの幅をxの関数とみて表したもの×dx」
のこと. ![]() はyの関数×dyです.
はyの関数×dyです.
※特に今の場合左右対称であれば, ![]() は, 面積要素が偶関数, 重み(x)が奇関数で, その積は奇関数. つまり積分値0になります.
は, 面積要素が偶関数, 重み(x)が奇関数で, その積は奇関数. つまり積分値0になります.
e.g.1
![]() . x軸中心に回転させて単位球の体積を得る.
. x軸中心に回転させて単位球の体積を得る.
対称性から![]() . よって
. よって![]() を求める. y方向への面積要素は, yを固定した時の切り口の長さ×dyだから,
を求める. y方向への面積要素は, yを固定した時の切り口の長さ×dyだから, ![]() の差を取って
の差を取って![]() を得る. そこで重心から回転軸までの距離Lはそのまま重心のy座標でよくて,
を得る. そこで重心から回転軸までの距離Lはそのまま重心のy座標でよくて,
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} L &=& S^{-1} g_y \\ &=& S^{-1} \int_0^1 2y \sqrt{1-y^2}dy \\ &=& 2S^{-1} \int_0^{\pi/2} \sin\theta cos^2\theta d\theta \\ &=& 2S^{-1} \int_0^{\pi/2} d(-\cos\theta)- \sin^3\theta d\theta \\ &=& 2S^{-1} ( 1 - \int_0^{\pi/2} \sin^3\theta d\theta ) \\ &=& 2S^{-1} ( 1 - 2/3 ) = S^{-1}2/3 \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-90432e7cea7ff36253e1185be450e107_l3.png)
よって![]() .
.
※途中の計算にはWallisの公式![]() を使うなどして早く解けるようにするのが良い(
を使うなどして早く解けるようにするのが良い(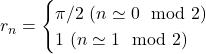 )
)
e.g.2
![]() と
と![]() とで囲まれた部分を
とで囲まれた部分を![]() を軸に回転させた体積. つまり
を軸に回転させた体積. つまり![]() のグラフを原点中心に
のグラフを原点中心に![]() 回転させたものの第一象限にある部分.
回転させたものの第一象限にある部分.
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} (x,\cosh(x)-1)&\mapsto& \begin{pmatrix}\cos(3/4\pi) & -\sin(3/4\pi)\\ \sin(3/4\pi) & \cos(3/4\pi)\end{pmatrix}{}^t(x,\cosh(x)-1) \\ &=&\psi(x) \\ &=& 1/\sqrt{2}\begin{pmatrix} -x-\cosh(x)+1 \\ x-\cosh(x)+1\end{pmatrix} \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-595a99608c74ad71ab94cdd2464b016d_l3.png)
が曲線を定めるのだが, これはグラフ
から分かるように, x=0ともう一つx=8/5付近で零点を持つ. この点をρと書くことにする.
![Rendered by QuickLaTeX.com \[\tau(x)=\begin{cases} (0,2x\rho) & (0\leq x \leq 1/2)\\ \psi(2\rho (1-x)) & (1/2\leq x \leq 1) \end{cases}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-56fec62eeb152d415b88abe1031f3c29_l3.png)
と定義すると, 弧のベクトル場を定義する![]() 級ベクトル値関数である. グリーンの定理の帰結から,
級ベクトル値関数である. グリーンの定理の帰結から, ![]() である(ここで
である(ここで![]() となるよう適当に選べば,
となるよう適当に選べば, ![]() として良い).
として良い).
![]() 等となるが,
等となるが, ![]() において左辺が0になるのでこれは省くと,
において左辺が0になるのでこれは省くと,
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} && \int_{1/2}^1 G(\tau(t))\tau'(t)dt \\ &=& \frac{\rho\sqrt{2}}{4} (\sinh(2\rho(1-t))-1)(2\rho(1-t)+\cosh(2\rho(1-t))-1)^2 \end{array}\]](https://blog.icefog.work/wp-content/ql-cache/quicklatex.com-0f100e2fe42215b5dc52926e1c737642_l3.png)
等となる. 計算は非常に複雑だが, この方法で線積分に帰着させることができる.
————————-
2015/03/15 00:30:53
関数が多価の場合に有用ではあるが, 線積分に依らないと正しい値はでないことが, 後で簡単な考察により分かった. 多価の部分を切り詰めると体積が小さくなってしまうから.
