用途に合う構造 (e.g. 形式や型) を与えたデータは (c.f. モデリング)、蓄積された時に表す意味を解釈しやすい。
現実の世界では全てのデータにこうした構造を与えられる訳ではなく、また個々のデータに構造が与えられていたとしても塊として意味を成さないものも多い。
データの集まりを (有限の) 点と構造に分離した時、データの有限点の集合[1]しばしば現実の物体の境界を近似する場合に使われる。をpoint-cloud dataと言い、構造[2]しばしば実三次元空間の部分空間が使われる。をunderlying space (of data)と言う。以降データの集まりを:
- point-cloud: V,
- underlying space: X,
- embedding:
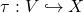 .
.
の組で![]() と表すことにする。
と表すことにする。
ここで採用した定義は、幾何的な対象に限定されるものではない。実際以下のようなデータ:
| 顧客ID | 顧客姓 | 顧客名 | 顧客国籍 | 顧客年齢 |
|---|---|---|---|---|
| 394934 | Sudo | Ako | Japan | 32 |
| 109214 | Ito | Iko | Japan | 24 |
| 210143 | Sato | Uo | Japan | 13 |
| 202148 | Davidson | Edward | America | 22 |
| 810714 | Shiing | Chern | China | 71 |
| … | … | … | … | … |
を恣意的に、又は適当なDRT[3]Dimensionality Reduction Techniquesの略。によって国籍と年齢に制限すると、このデータは![]() と表現される[4]最適なDRT、そして与えられた生のデータの表現を与える問題一つ一つが大きなトピックで、この記事では踏み込まない。表現問題はCategory … Continue reading。
と表現される[4]最適なDRT、そして与えられた生のデータの表現を与える問題一つ一つが大きなトピックで、この記事では踏み込まない。表現問題はCategory … Continue reading。
一般のデータ分類問題[5]構造の無い現実の生データから、誘導されるtopology invariantな特徴を抽出する問題。の一つの解釈として、次のようなFunctor (の合成) が考えられる:
![]()
記号が多いのでその定義は以下表でまとめた。
| 項番 | 記号 | 定義 | 解釈 |
|---|---|---|---|
| 1 | Arrow category of a subcategory of | Point-cloud data and its underlying unstructured total set. | |
| 2 | Arrow category of a subcategory of | Point-cloud data and its underlying space. | |
| 3 | Category of simplicial set. | Combinatorial representation of topologized data. | |
| 4 | Abelian category. | Represents a value of classification. | |
| 5 | P | A faithful topological translation. | Responsible for the reduction, optimization and possible structurization (e.g. metric) of data. |
| 6 | Q | A composition functor of simplicial interpretation followed by the forgetful functor that discards canonical inclusion of vertices. | Give a combinatorial interpretation of data along with parameters responsible for homotopy persistence. |
| 7 | R | Dold-Kan correspondence followed by a choice functor of the object with global persistence for given parameter. | Give a reduced representation of evaluated class of data. |
記号表の項番3以降の対象とそれに付随する問題については個人的な興味があり、特に5と6は私のバックボーンからしてしばしば研究の対象になる。
今回は6について、以下の Witness ComplexのSimulator (PC推奨) で次の事を直感的に体感できるプログラムを作ってみたので、興味がある方は試してみると面白いと思う:
- 円を粗くなぞる様に配置されたpoint-cloud data (黒い点) に対し, 初期化処理でランダムに頂点 (赤い点, landmarks) を配置する;
+Rボタンを何度か押し半径を大きくしていくと, いずれ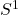 にホモトピー同値なSimplicial Complexを得る(各Simplex
にホモトピー同値なSimplicial Complexを得る(各Simplex 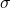 が表れる最小の半径Rを
が表れる最小の半径Rを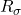 と書き, [Silva]では
と書き, [Silva]では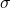 のtime of appearanceと呼んでいる);[6]初期化時の頂点の配置が偏り過ぎていると, 期待したホモトピー型 ()を持つSimplicial Complexに到達するまでに大きな半径を要することがある. … Continue reading
のtime of appearanceと呼んでいる);[6]初期化時の頂点の配置が偏り過ぎていると, 期待したホモトピー型 ()を持つSimplicial Complexに到達するまでに大きな半径を要することがある. … Continue reading
Persistent Homologyの理論では, (PH Barcode Decompositionにおいて) 最も長く持続したホモトピー型[7]この場合半径Rで添字付けられたSimplicial Complexesのfiltrationの, 各Rにおけるホモトピー型.を意味のあるデータとして重要視するが、注意深く選択したパラメタを採用した特別な事例において、殆ど全ての試行でこのデータが期待されたものと整合するという結果が示されている(c.f. [Silva])。
また以下の動画は、乱数で与えられたpoint-cloud dataに対し、幾つかのパラメタを動かして変化するSimplicial Decompositionの様子を観察できるように作成した。
Footnotes
| ↑1 | しばしば現実の物体の境界を近似する場合に使われる。 |
|---|---|
| ↑2 | しばしば実三次元空間の部分空間が使われる。 |
| ↑3 | Dimensionality Reduction Techniquesの略。 |
| ↑4 | 最適なDRT、そして与えられた生のデータの表現を与える問題一つ一つが大きなトピックで、この記事では踏み込まない。表現問題はCategory |
| ↑5 | 構造の無い現実の生データから、誘導されるtopology invariantな特徴を抽出する問題。 |
| ↑6 | 初期化時の頂点の配置が偏り過ぎていると, 期待したホモトピー型 ( |
| ↑7 | この場合半径Rで添字付けられたSimplicial Complexesのfiltrationの, 各Rにおけるホモトピー型. |